%global _empty_manifest_terminate_build 0
Name: python-gstools
Version: 1.4.1
Release: 1
Summary: GSTools: A geostatistical toolbox.
License: LGPL-3.0
URL: https://geostat-framework.org/#gstools
Source0: https://mirrors.nju.edu.cn/pypi/web/packages/18/fb/9ac3d888a17109c61645021c797b3c2ea022626f62ee8e4a7351594eb9f8/gstools-1.4.1.tar.gz
Requires: python3-emcee
Requires: python3-hankel
Requires: python3-meshio
Requires: python3-numpy
Requires: python3-pyevtk
Requires: python3-scipy
Requires: python3-m2r2
Requires: python3-matplotlib
Requires: python3-meshzoo
Requires: python3-numpydoc
Requires: python3-pykrige
Requires: python3-pyvista
Requires: python3-sphinx
Requires: python3-sphinx-gallery
Requires: python3-sphinx-rtd-theme
Requires: python3-sphinxcontrib-youtube
Requires: python3-matplotlib
Requires: python3-pyvista
Requires: python3-gstools-core
Requires: python3-pytest-cov
%description
# Welcome to GSTools
[](https://doi.org/10.5194/gmd-15-3161-2022)
[](https://doi.org/10.5281/zenodo.1313628)
[](https://badge.fury.io/py/gstools)
[](https://anaconda.org/conda-forge/gstools)
[](https://github.com/GeoStat-Framework/GSTools/actions)
[](https://coveralls.io/github/GeoStat-Framework/GSTools?branch=main)
[](https://geostat-framework.readthedocs.io/projects/gstools/en/stable/?badge=stable)
[](https://github.com/ambv/black)

Get in Touch!





Youtube Tutorial on GSTools
## Purpose
 GeoStatTools provides geostatistical tools for various purposes:
- random field generation
- simple, ordinary, universal and external drift kriging
- conditioned field generation
- incompressible random vector field generation
- (automated) variogram estimation and fitting
- directional variogram estimation and modelling
- data normalization and transformation
- many readily provided and even user-defined covariance models
- metric spatio-temporal modelling
- plotting and exporting routines
## Installation
### conda
GSTools can be installed via [conda][conda_link] on Linux, Mac, and Windows.
Install the package by typing the following command in a command terminal:
conda install gstools
In case conda forge is not set up for your system yet, see the easy to follow
instructions on [conda forge][conda_forge_link]. Using conda, the parallelized
version of GSTools should be installed.
### pip
GSTools can be installed via [pip][pip_link] on Linux, Mac, and Windows.
On Windows you can install [WinPython][winpy_link] to get Python and pip
running. Install the package by typing the following command in a command terminal:
pip install gstools
To install the latest development version via pip, see the
[documentation][doc_install_link].
## Citation
If you are using GSTools in your publication please cite our paper:
> Müller, S., Schüler, L., Zech, A., and Heße, F.:
> GSTools v1.3: a toolbox for geostatistical modelling in Python,
> Geosci. Model Dev., 15, 3161–3182, https://doi.org/10.5194/gmd-15-3161-2022, 2022.
You can cite the Zenodo code publication of GSTools by:
> Sebastian Müller & Lennart Schüler. GeoStat-Framework/GSTools. Zenodo. https://doi.org/10.5281/zenodo.1313628
If you want to cite a specific version, have a look at the [Zenodo site](https://doi.org/10.5281/zenodo.1313628).
## Documentation for GSTools
You can find the documentation under [geostat-framework.readthedocs.io][doc_link].
### Tutorials and Examples
The documentation also includes some [tutorials][tut_link], showing the most important use cases of GSTools, which are
- [Random Field Generation][tut1_link]
- [The Covariance Model][tut2_link]
- [Variogram Estimation][tut3_link]
- [Random Vector Field Generation][tut4_link]
- [Kriging][tut5_link]
- [Conditioned random field generation][tut6_link]
- [Field transformations][tut7_link]
- [Geographic Coordinates][tut8_link]
- [Spatio-Temporal Modelling][tut9_link]
- [Normalizing Data][tut10_link]
- [Miscellaneous examples][tut0_link]
The associated python scripts are provided in the `examples` folder.
## Spatial Random Field Generation
The core of this library is the generation of spatial random fields. These fields are generated using the randomisation method, described by [Heße et al. 2014][rand_link].
[rand_link]: https://doi.org/10.1016/j.envsoft.2014.01.013
### Examples
#### Gaussian Covariance Model
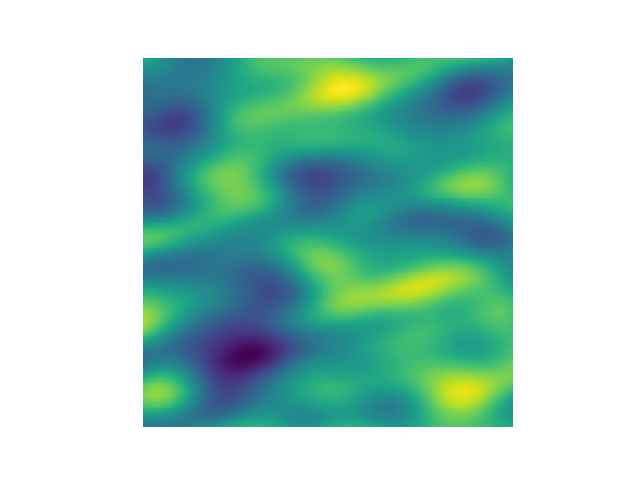
This is an example of how to generate a 2 dimensional spatial random field with a gaussian covariance model.
```python
import gstools as gs
# structured field with a size 100x100 and a grid-size of 1x1
x = y = range(100)
model = gs.Gaussian(dim=2, var=1, len_scale=10)
srf = gs.SRF(model)
srf((x, y), mesh_type='structured')
srf.plot()
```
GeoStatTools provides geostatistical tools for various purposes:
- random field generation
- simple, ordinary, universal and external drift kriging
- conditioned field generation
- incompressible random vector field generation
- (automated) variogram estimation and fitting
- directional variogram estimation and modelling
- data normalization and transformation
- many readily provided and even user-defined covariance models
- metric spatio-temporal modelling
- plotting and exporting routines
## Installation
### conda
GSTools can be installed via [conda][conda_link] on Linux, Mac, and Windows.
Install the package by typing the following command in a command terminal:
conda install gstools
In case conda forge is not set up for your system yet, see the easy to follow
instructions on [conda forge][conda_forge_link]. Using conda, the parallelized
version of GSTools should be installed.
### pip
GSTools can be installed via [pip][pip_link] on Linux, Mac, and Windows.
On Windows you can install [WinPython][winpy_link] to get Python and pip
running. Install the package by typing the following command in a command terminal:
pip install gstools
To install the latest development version via pip, see the
[documentation][doc_install_link].
## Citation
If you are using GSTools in your publication please cite our paper:
> Müller, S., Schüler, L., Zech, A., and Heße, F.:
> GSTools v1.3: a toolbox for geostatistical modelling in Python,
> Geosci. Model Dev., 15, 3161–3182, https://doi.org/10.5194/gmd-15-3161-2022, 2022.
You can cite the Zenodo code publication of GSTools by:
> Sebastian Müller & Lennart Schüler. GeoStat-Framework/GSTools. Zenodo. https://doi.org/10.5281/zenodo.1313628
If you want to cite a specific version, have a look at the [Zenodo site](https://doi.org/10.5281/zenodo.1313628).
## Documentation for GSTools
You can find the documentation under [geostat-framework.readthedocs.io][doc_link].
### Tutorials and Examples
The documentation also includes some [tutorials][tut_link], showing the most important use cases of GSTools, which are
- [Random Field Generation][tut1_link]
- [The Covariance Model][tut2_link]
- [Variogram Estimation][tut3_link]
- [Random Vector Field Generation][tut4_link]
- [Kriging][tut5_link]
- [Conditioned random field generation][tut6_link]
- [Field transformations][tut7_link]
- [Geographic Coordinates][tut8_link]
- [Spatio-Temporal Modelling][tut9_link]
- [Normalizing Data][tut10_link]
- [Miscellaneous examples][tut0_link]
The associated python scripts are provided in the `examples` folder.
## Spatial Random Field Generation
The core of this library is the generation of spatial random fields. These fields are generated using the randomisation method, described by [Heße et al. 2014][rand_link].
[rand_link]: https://doi.org/10.1016/j.envsoft.2014.01.013
### Examples
#### Gaussian Covariance Model
This is an example of how to generate a 2 dimensional spatial random field with a gaussian covariance model.
```python
import gstools as gs
# structured field with a size 100x100 and a grid-size of 1x1
x = y = range(100)
model = gs.Gaussian(dim=2, var=1, len_scale=10)
srf = gs.SRF(model)
srf((x, y), mesh_type='structured')
srf.plot()
```
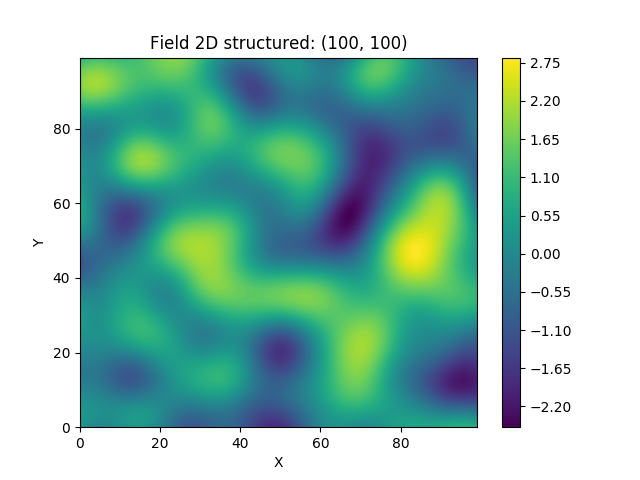
GSTools also provides support for [geographic coordinates](https://en.wikipedia.org/wiki/Geographic_coordinate_system).
This works perfectly well with [cartopy](https://scitools.org.uk/cartopy/docs/latest/index.html).
```python
import matplotlib.pyplot as plt
import cartopy.crs as ccrs
import gstools as gs
# define a structured field by latitude and longitude
lat = lon = range(-80, 81)
model = gs.Gaussian(latlon=True, len_scale=777, rescale=gs.EARTH_RADIUS)
srf = gs.SRF(model, seed=12345)
field = srf.structured((lat, lon))
# Orthographic plotting with cartopy
ax = plt.subplot(projection=ccrs.Orthographic(-45, 45))
cont = ax.contourf(lon, lat, field, transform=ccrs.PlateCarree())
ax.coastlines()
ax.set_global()
plt.colorbar(cont)
```

A similar example but for a three dimensional field is exported to a [VTK](https://vtk.org/) file, which can be visualized with [ParaView](https://www.paraview.org/) or [PyVista](https://docs.pyvista.org) in Python:
```python
import gstools as gs
# structured field with a size 100x100x100 and a grid-size of 1x1x1
x = y = z = range(100)
model = gs.Gaussian(dim=3, len_scale=[16, 8, 4], angles=(0.8, 0.4, 0.2))
srf = gs.SRF(model)
srf((x, y, z), mesh_type='structured')
srf.vtk_export('3d_field') # Save to a VTK file for ParaView
mesh = srf.to_pyvista() # Create a PyVista mesh for plotting in Python
mesh.contour(isosurfaces=8).plot()
```

## Estimating and Fitting Variograms
The spatial structure of a field can be analyzed with the variogram, which contains the same information as the covariance function.
All covariance models can be used to fit given variogram data by a simple interface.
### Example
This is an example of how to estimate the variogram of a 2 dimensional unstructured field and estimate the parameters of the covariance
model again.
```python
import numpy as np
import gstools as gs
# generate a synthetic field with an exponential model
x = np.random.RandomState(19970221).rand(1000) * 100.
y = np.random.RandomState(20011012).rand(1000) * 100.
model = gs.Exponential(dim=2, var=2, len_scale=8)
srf = gs.SRF(model, mean=0, seed=19970221)
field = srf((x, y))
# estimate the variogram of the field
bin_center, gamma = gs.vario_estimate((x, y), field)
# fit the variogram with a stable model. (no nugget fitted)
fit_model = gs.Stable(dim=2)
fit_model.fit_variogram(bin_center, gamma, nugget=False)
# output
ax = fit_model.plot(x_max=max(bin_center))
ax.scatter(bin_center, gamma)
print(fit_model)
```
Which gives:
```python
Stable(dim=2, var=1.85, len_scale=7.42, nugget=0.0, anis=[1.0], angles=[0.0], alpha=1.09)
```

## Kriging and Conditioned Random Fields
An important part of geostatistics is Kriging and conditioning spatial random
fields to measurements. With conditioned random fields, an ensemble of field realizations with their variability depending on the proximity of the measurements can be generated.
### Example
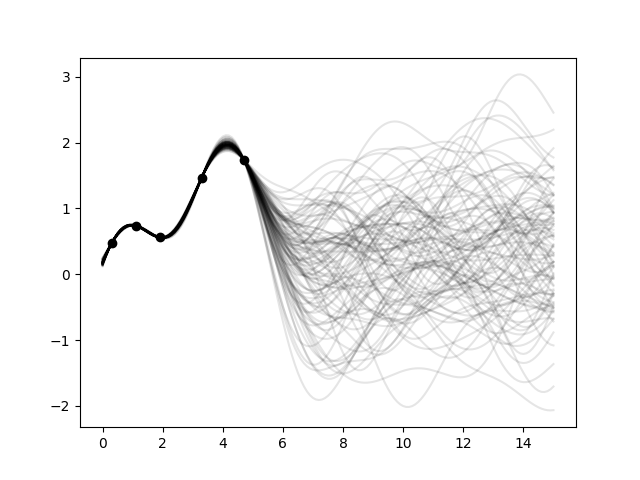
For better visualization, we will condition a 1d field to a few "measurements", generate 100 realizations and plot them:
```python
import numpy as np
import matplotlib.pyplot as plt
import gstools as gs
# conditions
cond_pos = [0.3, 1.9, 1.1, 3.3, 4.7]
cond_val = [0.47, 0.56, 0.74, 1.47, 1.74]
# conditioned spatial random field class
model = gs.Gaussian(dim=1, var=0.5, len_scale=2)
krige = gs.krige.Ordinary(model, cond_pos, cond_val)
cond_srf = gs.CondSRF(krige)
# same output positions for all ensemble members
grid_pos = np.linspace(0.0, 15.0, 151)
cond_srf.set_pos(grid_pos)
# seeded ensemble generation
seed = gs.random.MasterRNG(20170519)
for i in range(100):
field = cond_srf(seed=seed(), store=f"field_{i}")
plt.plot(grid_pos, field, color="k", alpha=0.1)
plt.scatter(cond_pos, cond_val, color="k")
plt.show()
```
## User Defined Covariance Models
One of the core-features of GSTools is the powerful
[CovModel][cov_link]
class, which allows to easy define covariance models by the user.
### Example
Here we re-implement the Gaussian covariance model by defining just a
[correlation][cor_link] function, which takes a non-dimensional distance ``h = r/l``:
```python
import numpy as np
import gstools as gs
# use CovModel as the base-class
class Gau(gs.CovModel):
def cor(self, h):
return np.exp(-h**2)
```
And that's it! With ``Gau`` you now have a fully working covariance model,
which you could use for field generation or variogram fitting as shown above.
Have a look at the [documentation ][doc_link] for further information on incorporating
optional parameters and optimizations.
## Incompressible Vector Field Generation
Using the original [Kraichnan method][kraichnan_link], incompressible random
spatial vector fields can be generated.
### Example
```python
import numpy as np
import gstools as gs
x = np.arange(100)
y = np.arange(100)
model = gs.Gaussian(dim=2, var=1, len_scale=10)
srf = gs.SRF(model, generator='VectorField', seed=19841203)
srf((x, y), mesh_type='structured')
srf.plot()
```
yielding
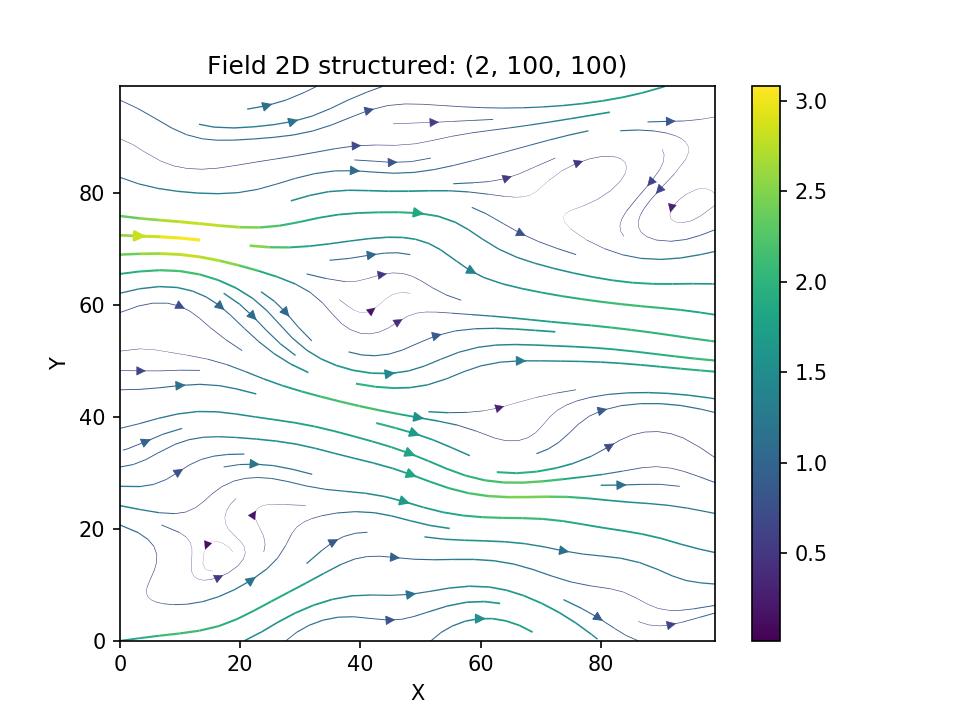
[kraichnan_link]: https://doi.org/10.1063/1.1692799
## VTK/PyVista Export
After you have created a field, you may want to save it to file, so we provide
a handy [VTK][vtk_link] export routine using the `.vtk_export()` or you could
create a VTK/PyVista dataset for use in Python with to `.to_pyvista()` method:
```python
import gstools as gs
x = y = range(100)
model = gs.Gaussian(dim=2, var=1, len_scale=10)
srf = gs.SRF(model)
srf((x, y), mesh_type='structured')
srf.vtk_export("field") # Saves to a VTK file
mesh = srf.to_pyvista() # Create a VTK/PyVista dataset in memory
mesh.plot()
```
Which gives a RectilinearGrid VTK file ``field.vtr`` or creates a PyVista mesh
in memory for immediate 3D plotting in Python.
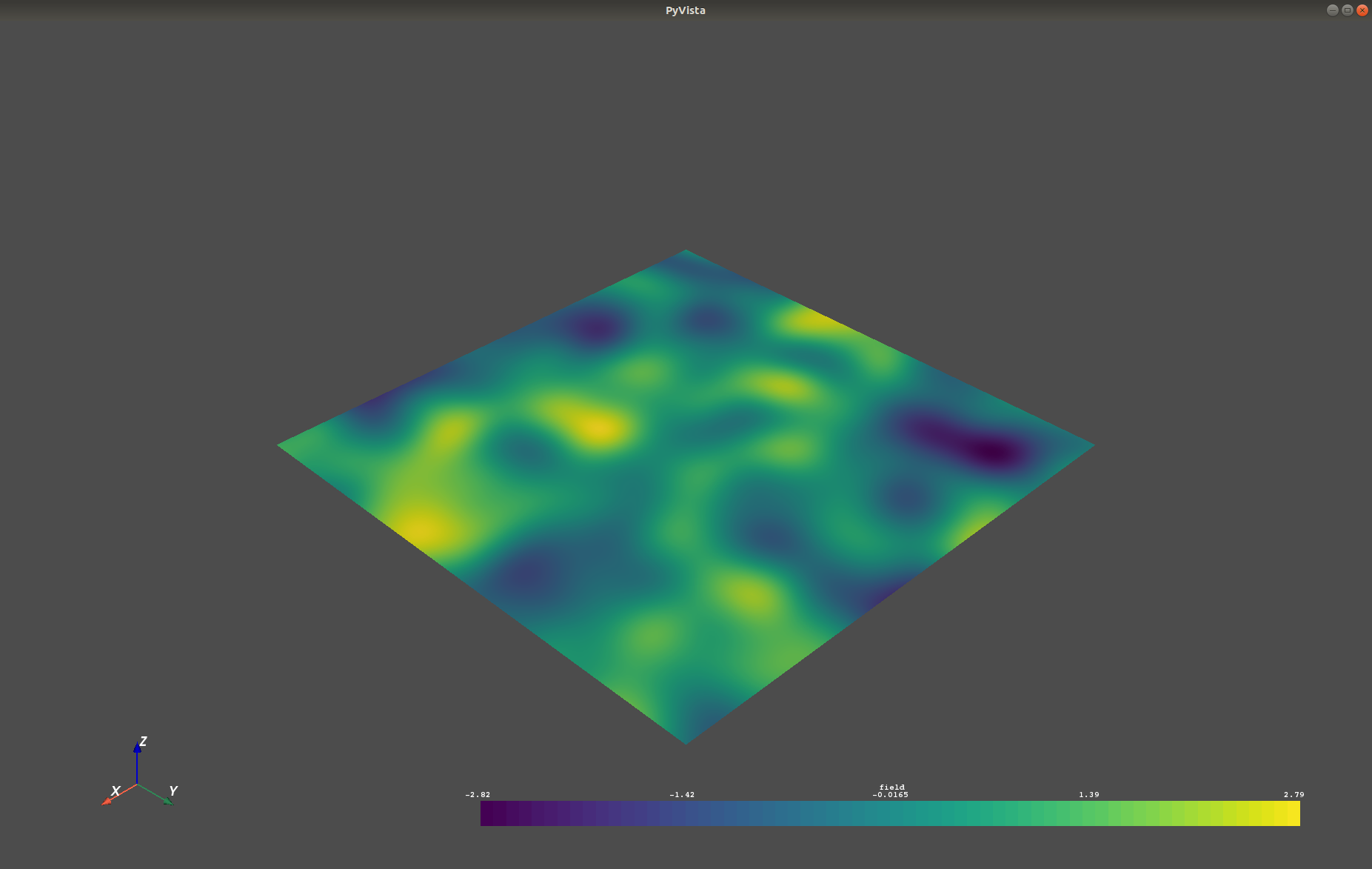
## Requirements:
- [NumPy >= 1.14.5](https://www.numpy.org)
- [SciPy >= 1.1.0](https://www.scipy.org/scipylib)
- [hankel >= 1.0.0](https://github.com/steven-murray/hankel)
- [emcee >= 3.0.0](https://github.com/dfm/emcee)
- [pyevtk >= 1.1.1](https://github.com/pyscience-projects/pyevtk)
- [meshio >= 5.1.0](https://github.com/nschloe/meshio)
### Optional
- [GSTools-Core >= 0.2.0](https://github.com/GeoStat-Framework/GSTools-Core)
- [matplotlib](https://matplotlib.org)
- [pyvista](https://docs.pyvista.org/)
## Contact
You can contact us via .
## License
[LGPLv3][license_link] © 2018-2021
[pip_link]: https://pypi.org/project/gstools
[conda_link]: https://docs.conda.io/en/latest/miniconda.html
[conda_forge_link]: https://github.com/conda-forge/gstools-feedstock#installing-gstools
[conda_pip]: https://docs.conda.io/projects/conda/en/latest/user-guide/tasks/manage-pkgs.html#installing-non-conda-packages
[pipiflag]: https://pip-python3.readthedocs.io/en/latest/reference/pip_install.html?highlight=i#cmdoption-i
[winpy_link]: https://winpython.github.io/
[license_link]: https://github.com/GeoStat-Framework/GSTools/blob/main/LICENSE
[cov_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/generated/gstools.covmodel.CovModel.html#gstools.covmodel.CovModel
[stable_link]: https://en.wikipedia.org/wiki/Stable_distribution
[doc_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/
[doc_install_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/#pip
[tut_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/tutorials.html
[tut1_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/examples/01_random_field/index.html
[tut2_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/examples/02_cov_model/index.html
[tut3_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/examples/03_variogram/index.html
[tut4_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/examples/04_vector_field/index.html
[tut5_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/examples/05_kriging/index.html
[tut6_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/examples/06_conditioned_fields/index.html
[tut7_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/examples/07_transformations/index.html
[tut8_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/examples/08_geo_coordinates/index.html
[tut9_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/examples/09_spatio_temporal/index.html
[tut10_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/examples/10_normalizer/index.html
[tut0_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/examples/00_misc/index.html
[cor_link]: https://en.wikipedia.org/wiki/Autocovariance#Normalization
[vtk_link]: https://www.vtk.org/
%package -n python3-gstools
Summary: GSTools: A geostatistical toolbox.
Provides: python-gstools
BuildRequires: python3-devel
BuildRequires: python3-setuptools
BuildRequires: python3-pip
BuildRequires: python3-cffi
BuildRequires: gcc
BuildRequires: gdb
%description -n python3-gstools
# Welcome to GSTools
[](https://doi.org/10.5194/gmd-15-3161-2022)
[](https://doi.org/10.5281/zenodo.1313628)
[](https://badge.fury.io/py/gstools)
[](https://anaconda.org/conda-forge/gstools)
[](https://github.com/GeoStat-Framework/GSTools/actions)
[](https://coveralls.io/github/GeoStat-Framework/GSTools?branch=main)
[](https://geostat-framework.readthedocs.io/projects/gstools/en/stable/?badge=stable)
[](https://github.com/ambv/black)

Get in Touch!





Youtube Tutorial on GSTools

## Purpose
 GeoStatTools provides geostatistical tools for various purposes:
- random field generation
- simple, ordinary, universal and external drift kriging
- conditioned field generation
- incompressible random vector field generation
- (automated) variogram estimation and fitting
- directional variogram estimation and modelling
- data normalization and transformation
- many readily provided and even user-defined covariance models
- metric spatio-temporal modelling
- plotting and exporting routines
## Installation
### conda
GSTools can be installed via [conda][conda_link] on Linux, Mac, and Windows.
Install the package by typing the following command in a command terminal:
conda install gstools
In case conda forge is not set up for your system yet, see the easy to follow
instructions on [conda forge][conda_forge_link]. Using conda, the parallelized
version of GSTools should be installed.
### pip
GSTools can be installed via [pip][pip_link] on Linux, Mac, and Windows.
On Windows you can install [WinPython][winpy_link] to get Python and pip
running. Install the package by typing the following command in a command terminal:
pip install gstools
To install the latest development version via pip, see the
[documentation][doc_install_link].
## Citation
If you are using GSTools in your publication please cite our paper:
> Müller, S., Schüler, L., Zech, A., and Heße, F.:
> GSTools v1.3: a toolbox for geostatistical modelling in Python,
> Geosci. Model Dev., 15, 3161–3182, https://doi.org/10.5194/gmd-15-3161-2022, 2022.
You can cite the Zenodo code publication of GSTools by:
> Sebastian Müller & Lennart Schüler. GeoStat-Framework/GSTools. Zenodo. https://doi.org/10.5281/zenodo.1313628
If you want to cite a specific version, have a look at the [Zenodo site](https://doi.org/10.5281/zenodo.1313628).
## Documentation for GSTools
You can find the documentation under [geostat-framework.readthedocs.io][doc_link].
### Tutorials and Examples
The documentation also includes some [tutorials][tut_link], showing the most important use cases of GSTools, which are
- [Random Field Generation][tut1_link]
- [The Covariance Model][tut2_link]
- [Variogram Estimation][tut3_link]
- [Random Vector Field Generation][tut4_link]
- [Kriging][tut5_link]
- [Conditioned random field generation][tut6_link]
- [Field transformations][tut7_link]
- [Geographic Coordinates][tut8_link]
- [Spatio-Temporal Modelling][tut9_link]
- [Normalizing Data][tut10_link]
- [Miscellaneous examples][tut0_link]
The associated python scripts are provided in the `examples` folder.
## Spatial Random Field Generation
The core of this library is the generation of spatial random fields. These fields are generated using the randomisation method, described by [Heße et al. 2014][rand_link].
[rand_link]: https://doi.org/10.1016/j.envsoft.2014.01.013
### Examples
#### Gaussian Covariance Model
This is an example of how to generate a 2 dimensional spatial random field with a gaussian covariance model.
```python
import gstools as gs
# structured field with a size 100x100 and a grid-size of 1x1
x = y = range(100)
model = gs.Gaussian(dim=2, var=1, len_scale=10)
srf = gs.SRF(model)
srf((x, y), mesh_type='structured')
srf.plot()
```
GeoStatTools provides geostatistical tools for various purposes:
- random field generation
- simple, ordinary, universal and external drift kriging
- conditioned field generation
- incompressible random vector field generation
- (automated) variogram estimation and fitting
- directional variogram estimation and modelling
- data normalization and transformation
- many readily provided and even user-defined covariance models
- metric spatio-temporal modelling
- plotting and exporting routines
## Installation
### conda
GSTools can be installed via [conda][conda_link] on Linux, Mac, and Windows.
Install the package by typing the following command in a command terminal:
conda install gstools
In case conda forge is not set up for your system yet, see the easy to follow
instructions on [conda forge][conda_forge_link]. Using conda, the parallelized
version of GSTools should be installed.
### pip
GSTools can be installed via [pip][pip_link] on Linux, Mac, and Windows.
On Windows you can install [WinPython][winpy_link] to get Python and pip
running. Install the package by typing the following command in a command terminal:
pip install gstools
To install the latest development version via pip, see the
[documentation][doc_install_link].
## Citation
If you are using GSTools in your publication please cite our paper:
> Müller, S., Schüler, L., Zech, A., and Heße, F.:
> GSTools v1.3: a toolbox for geostatistical modelling in Python,
> Geosci. Model Dev., 15, 3161–3182, https://doi.org/10.5194/gmd-15-3161-2022, 2022.
You can cite the Zenodo code publication of GSTools by:
> Sebastian Müller & Lennart Schüler. GeoStat-Framework/GSTools. Zenodo. https://doi.org/10.5281/zenodo.1313628
If you want to cite a specific version, have a look at the [Zenodo site](https://doi.org/10.5281/zenodo.1313628).
## Documentation for GSTools
You can find the documentation under [geostat-framework.readthedocs.io][doc_link].
### Tutorials and Examples
The documentation also includes some [tutorials][tut_link], showing the most important use cases of GSTools, which are
- [Random Field Generation][tut1_link]
- [The Covariance Model][tut2_link]
- [Variogram Estimation][tut3_link]
- [Random Vector Field Generation][tut4_link]
- [Kriging][tut5_link]
- [Conditioned random field generation][tut6_link]
- [Field transformations][tut7_link]
- [Geographic Coordinates][tut8_link]
- [Spatio-Temporal Modelling][tut9_link]
- [Normalizing Data][tut10_link]
- [Miscellaneous examples][tut0_link]
The associated python scripts are provided in the `examples` folder.
## Spatial Random Field Generation
The core of this library is the generation of spatial random fields. These fields are generated using the randomisation method, described by [Heße et al. 2014][rand_link].
[rand_link]: https://doi.org/10.1016/j.envsoft.2014.01.013
### Examples
#### Gaussian Covariance Model
This is an example of how to generate a 2 dimensional spatial random field with a gaussian covariance model.
```python
import gstools as gs
# structured field with a size 100x100 and a grid-size of 1x1
x = y = range(100)
model = gs.Gaussian(dim=2, var=1, len_scale=10)
srf = gs.SRF(model)
srf((x, y), mesh_type='structured')
srf.plot()
```

GSTools also provides support for [geographic coordinates](https://en.wikipedia.org/wiki/Geographic_coordinate_system).
This works perfectly well with [cartopy](https://scitools.org.uk/cartopy/docs/latest/index.html).
```python
import matplotlib.pyplot as plt
import cartopy.crs as ccrs
import gstools as gs
# define a structured field by latitude and longitude
lat = lon = range(-80, 81)
model = gs.Gaussian(latlon=True, len_scale=777, rescale=gs.EARTH_RADIUS)
srf = gs.SRF(model, seed=12345)
field = srf.structured((lat, lon))
# Orthographic plotting with cartopy
ax = plt.subplot(projection=ccrs.Orthographic(-45, 45))
cont = ax.contourf(lon, lat, field, transform=ccrs.PlateCarree())
ax.coastlines()
ax.set_global()
plt.colorbar(cont)
```

A similar example but for a three dimensional field is exported to a [VTK](https://vtk.org/) file, which can be visualized with [ParaView](https://www.paraview.org/) or [PyVista](https://docs.pyvista.org) in Python:
```python
import gstools as gs
# structured field with a size 100x100x100 and a grid-size of 1x1x1
x = y = z = range(100)
model = gs.Gaussian(dim=3, len_scale=[16, 8, 4], angles=(0.8, 0.4, 0.2))
srf = gs.SRF(model)
srf((x, y, z), mesh_type='structured')
srf.vtk_export('3d_field') # Save to a VTK file for ParaView
mesh = srf.to_pyvista() # Create a PyVista mesh for plotting in Python
mesh.contour(isosurfaces=8).plot()
```

## Estimating and Fitting Variograms
The spatial structure of a field can be analyzed with the variogram, which contains the same information as the covariance function.
All covariance models can be used to fit given variogram data by a simple interface.
### Example
This is an example of how to estimate the variogram of a 2 dimensional unstructured field and estimate the parameters of the covariance
model again.
```python
import numpy as np
import gstools as gs
# generate a synthetic field with an exponential model
x = np.random.RandomState(19970221).rand(1000) * 100.
y = np.random.RandomState(20011012).rand(1000) * 100.
model = gs.Exponential(dim=2, var=2, len_scale=8)
srf = gs.SRF(model, mean=0, seed=19970221)
field = srf((x, y))
# estimate the variogram of the field
bin_center, gamma = gs.vario_estimate((x, y), field)
# fit the variogram with a stable model. (no nugget fitted)
fit_model = gs.Stable(dim=2)
fit_model.fit_variogram(bin_center, gamma, nugget=False)
# output
ax = fit_model.plot(x_max=max(bin_center))
ax.scatter(bin_center, gamma)
print(fit_model)
```
Which gives:
```python
Stable(dim=2, var=1.85, len_scale=7.42, nugget=0.0, anis=[1.0], angles=[0.0], alpha=1.09)
```

## Kriging and Conditioned Random Fields
An important part of geostatistics is Kriging and conditioning spatial random
fields to measurements. With conditioned random fields, an ensemble of field realizations with their variability depending on the proximity of the measurements can be generated.
### Example
For better visualization, we will condition a 1d field to a few "measurements", generate 100 realizations and plot them:
```python
import numpy as np
import matplotlib.pyplot as plt
import gstools as gs
# conditions
cond_pos = [0.3, 1.9, 1.1, 3.3, 4.7]
cond_val = [0.47, 0.56, 0.74, 1.47, 1.74]
# conditioned spatial random field class
model = gs.Gaussian(dim=1, var=0.5, len_scale=2)
krige = gs.krige.Ordinary(model, cond_pos, cond_val)
cond_srf = gs.CondSRF(krige)
# same output positions for all ensemble members
grid_pos = np.linspace(0.0, 15.0, 151)
cond_srf.set_pos(grid_pos)
# seeded ensemble generation
seed = gs.random.MasterRNG(20170519)
for i in range(100):
field = cond_srf(seed=seed(), store=f"field_{i}")
plt.plot(grid_pos, field, color="k", alpha=0.1)
plt.scatter(cond_pos, cond_val, color="k")
plt.show()
```

## User Defined Covariance Models
One of the core-features of GSTools is the powerful
[CovModel][cov_link]
class, which allows to easy define covariance models by the user.
### Example
Here we re-implement the Gaussian covariance model by defining just a
[correlation][cor_link] function, which takes a non-dimensional distance ``h = r/l``:
```python
import numpy as np
import gstools as gs
# use CovModel as the base-class
class Gau(gs.CovModel):
def cor(self, h):
return np.exp(-h**2)
```
And that's it! With ``Gau`` you now have a fully working covariance model,
which you could use for field generation or variogram fitting as shown above.
Have a look at the [documentation ][doc_link] for further information on incorporating
optional parameters and optimizations.
## Incompressible Vector Field Generation
Using the original [Kraichnan method][kraichnan_link], incompressible random
spatial vector fields can be generated.
### Example
```python
import numpy as np
import gstools as gs
x = np.arange(100)
y = np.arange(100)
model = gs.Gaussian(dim=2, var=1, len_scale=10)
srf = gs.SRF(model, generator='VectorField', seed=19841203)
srf((x, y), mesh_type='structured')
srf.plot()
```
yielding

[kraichnan_link]: https://doi.org/10.1063/1.1692799
## VTK/PyVista Export
After you have created a field, you may want to save it to file, so we provide
a handy [VTK][vtk_link] export routine using the `.vtk_export()` or you could
create a VTK/PyVista dataset for use in Python with to `.to_pyvista()` method:
```python
import gstools as gs
x = y = range(100)
model = gs.Gaussian(dim=2, var=1, len_scale=10)
srf = gs.SRF(model)
srf((x, y), mesh_type='structured')
srf.vtk_export("field") # Saves to a VTK file
mesh = srf.to_pyvista() # Create a VTK/PyVista dataset in memory
mesh.plot()
```
Which gives a RectilinearGrid VTK file ``field.vtr`` or creates a PyVista mesh
in memory for immediate 3D plotting in Python.

## Requirements:
- [NumPy >= 1.14.5](https://www.numpy.org)
- [SciPy >= 1.1.0](https://www.scipy.org/scipylib)
- [hankel >= 1.0.0](https://github.com/steven-murray/hankel)
- [emcee >= 3.0.0](https://github.com/dfm/emcee)
- [pyevtk >= 1.1.1](https://github.com/pyscience-projects/pyevtk)
- [meshio >= 5.1.0](https://github.com/nschloe/meshio)
### Optional
- [GSTools-Core >= 0.2.0](https://github.com/GeoStat-Framework/GSTools-Core)
- [matplotlib](https://matplotlib.org)
- [pyvista](https://docs.pyvista.org/)
## Contact
You can contact us via .
## License
[LGPLv3][license_link] © 2018-2021
[pip_link]: https://pypi.org/project/gstools
[conda_link]: https://docs.conda.io/en/latest/miniconda.html
[conda_forge_link]: https://github.com/conda-forge/gstools-feedstock#installing-gstools
[conda_pip]: https://docs.conda.io/projects/conda/en/latest/user-guide/tasks/manage-pkgs.html#installing-non-conda-packages
[pipiflag]: https://pip-python3.readthedocs.io/en/latest/reference/pip_install.html?highlight=i#cmdoption-i
[winpy_link]: https://winpython.github.io/
[license_link]: https://github.com/GeoStat-Framework/GSTools/blob/main/LICENSE
[cov_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/generated/gstools.covmodel.CovModel.html#gstools.covmodel.CovModel
[stable_link]: https://en.wikipedia.org/wiki/Stable_distribution
[doc_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/
[doc_install_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/#pip
[tut_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/tutorials.html
[tut1_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/examples/01_random_field/index.html
[tut2_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/examples/02_cov_model/index.html
[tut3_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/examples/03_variogram/index.html
[tut4_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/examples/04_vector_field/index.html
[tut5_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/examples/05_kriging/index.html
[tut6_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/examples/06_conditioned_fields/index.html
[tut7_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/examples/07_transformations/index.html
[tut8_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/examples/08_geo_coordinates/index.html
[tut9_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/examples/09_spatio_temporal/index.html
[tut10_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/examples/10_normalizer/index.html
[tut0_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/examples/00_misc/index.html
[cor_link]: https://en.wikipedia.org/wiki/Autocovariance#Normalization
[vtk_link]: https://www.vtk.org/
%package help
Summary: Development documents and examples for gstools
Provides: python3-gstools-doc
%description help
# Welcome to GSTools
[](https://doi.org/10.5194/gmd-15-3161-2022)
[](https://doi.org/10.5281/zenodo.1313628)
[](https://badge.fury.io/py/gstools)
[](https://anaconda.org/conda-forge/gstools)
[](https://github.com/GeoStat-Framework/GSTools/actions)
[](https://coveralls.io/github/GeoStat-Framework/GSTools?branch=main)
[](https://geostat-framework.readthedocs.io/projects/gstools/en/stable/?badge=stable)
[](https://github.com/ambv/black)

Get in Touch!





Youtube Tutorial on GSTools

## Purpose
 GeoStatTools provides geostatistical tools for various purposes:
- random field generation
- simple, ordinary, universal and external drift kriging
- conditioned field generation
- incompressible random vector field generation
- (automated) variogram estimation and fitting
- directional variogram estimation and modelling
- data normalization and transformation
- many readily provided and even user-defined covariance models
- metric spatio-temporal modelling
- plotting and exporting routines
## Installation
### conda
GSTools can be installed via [conda][conda_link] on Linux, Mac, and Windows.
Install the package by typing the following command in a command terminal:
conda install gstools
In case conda forge is not set up for your system yet, see the easy to follow
instructions on [conda forge][conda_forge_link]. Using conda, the parallelized
version of GSTools should be installed.
### pip
GSTools can be installed via [pip][pip_link] on Linux, Mac, and Windows.
On Windows you can install [WinPython][winpy_link] to get Python and pip
running. Install the package by typing the following command in a command terminal:
pip install gstools
To install the latest development version via pip, see the
[documentation][doc_install_link].
## Citation
If you are using GSTools in your publication please cite our paper:
> Müller, S., Schüler, L., Zech, A., and Heße, F.:
> GSTools v1.3: a toolbox for geostatistical modelling in Python,
> Geosci. Model Dev., 15, 3161–3182, https://doi.org/10.5194/gmd-15-3161-2022, 2022.
You can cite the Zenodo code publication of GSTools by:
> Sebastian Müller & Lennart Schüler. GeoStat-Framework/GSTools. Zenodo. https://doi.org/10.5281/zenodo.1313628
If you want to cite a specific version, have a look at the [Zenodo site](https://doi.org/10.5281/zenodo.1313628).
## Documentation for GSTools
You can find the documentation under [geostat-framework.readthedocs.io][doc_link].
### Tutorials and Examples
The documentation also includes some [tutorials][tut_link], showing the most important use cases of GSTools, which are
- [Random Field Generation][tut1_link]
- [The Covariance Model][tut2_link]
- [Variogram Estimation][tut3_link]
- [Random Vector Field Generation][tut4_link]
- [Kriging][tut5_link]
- [Conditioned random field generation][tut6_link]
- [Field transformations][tut7_link]
- [Geographic Coordinates][tut8_link]
- [Spatio-Temporal Modelling][tut9_link]
- [Normalizing Data][tut10_link]
- [Miscellaneous examples][tut0_link]
The associated python scripts are provided in the `examples` folder.
## Spatial Random Field Generation
The core of this library is the generation of spatial random fields. These fields are generated using the randomisation method, described by [Heße et al. 2014][rand_link].
[rand_link]: https://doi.org/10.1016/j.envsoft.2014.01.013
### Examples
#### Gaussian Covariance Model
This is an example of how to generate a 2 dimensional spatial random field with a gaussian covariance model.
```python
import gstools as gs
# structured field with a size 100x100 and a grid-size of 1x1
x = y = range(100)
model = gs.Gaussian(dim=2, var=1, len_scale=10)
srf = gs.SRF(model)
srf((x, y), mesh_type='structured')
srf.plot()
```
GeoStatTools provides geostatistical tools for various purposes:
- random field generation
- simple, ordinary, universal and external drift kriging
- conditioned field generation
- incompressible random vector field generation
- (automated) variogram estimation and fitting
- directional variogram estimation and modelling
- data normalization and transformation
- many readily provided and even user-defined covariance models
- metric spatio-temporal modelling
- plotting and exporting routines
## Installation
### conda
GSTools can be installed via [conda][conda_link] on Linux, Mac, and Windows.
Install the package by typing the following command in a command terminal:
conda install gstools
In case conda forge is not set up for your system yet, see the easy to follow
instructions on [conda forge][conda_forge_link]. Using conda, the parallelized
version of GSTools should be installed.
### pip
GSTools can be installed via [pip][pip_link] on Linux, Mac, and Windows.
On Windows you can install [WinPython][winpy_link] to get Python and pip
running. Install the package by typing the following command in a command terminal:
pip install gstools
To install the latest development version via pip, see the
[documentation][doc_install_link].
## Citation
If you are using GSTools in your publication please cite our paper:
> Müller, S., Schüler, L., Zech, A., and Heße, F.:
> GSTools v1.3: a toolbox for geostatistical modelling in Python,
> Geosci. Model Dev., 15, 3161–3182, https://doi.org/10.5194/gmd-15-3161-2022, 2022.
You can cite the Zenodo code publication of GSTools by:
> Sebastian Müller & Lennart Schüler. GeoStat-Framework/GSTools. Zenodo. https://doi.org/10.5281/zenodo.1313628
If you want to cite a specific version, have a look at the [Zenodo site](https://doi.org/10.5281/zenodo.1313628).
## Documentation for GSTools
You can find the documentation under [geostat-framework.readthedocs.io][doc_link].
### Tutorials and Examples
The documentation also includes some [tutorials][tut_link], showing the most important use cases of GSTools, which are
- [Random Field Generation][tut1_link]
- [The Covariance Model][tut2_link]
- [Variogram Estimation][tut3_link]
- [Random Vector Field Generation][tut4_link]
- [Kriging][tut5_link]
- [Conditioned random field generation][tut6_link]
- [Field transformations][tut7_link]
- [Geographic Coordinates][tut8_link]
- [Spatio-Temporal Modelling][tut9_link]
- [Normalizing Data][tut10_link]
- [Miscellaneous examples][tut0_link]
The associated python scripts are provided in the `examples` folder.
## Spatial Random Field Generation
The core of this library is the generation of spatial random fields. These fields are generated using the randomisation method, described by [Heße et al. 2014][rand_link].
[rand_link]: https://doi.org/10.1016/j.envsoft.2014.01.013
### Examples
#### Gaussian Covariance Model
This is an example of how to generate a 2 dimensional spatial random field with a gaussian covariance model.
```python
import gstools as gs
# structured field with a size 100x100 and a grid-size of 1x1
x = y = range(100)
model = gs.Gaussian(dim=2, var=1, len_scale=10)
srf = gs.SRF(model)
srf((x, y), mesh_type='structured')
srf.plot()
```

GSTools also provides support for [geographic coordinates](https://en.wikipedia.org/wiki/Geographic_coordinate_system).
This works perfectly well with [cartopy](https://scitools.org.uk/cartopy/docs/latest/index.html).
```python
import matplotlib.pyplot as plt
import cartopy.crs as ccrs
import gstools as gs
# define a structured field by latitude and longitude
lat = lon = range(-80, 81)
model = gs.Gaussian(latlon=True, len_scale=777, rescale=gs.EARTH_RADIUS)
srf = gs.SRF(model, seed=12345)
field = srf.structured((lat, lon))
# Orthographic plotting with cartopy
ax = plt.subplot(projection=ccrs.Orthographic(-45, 45))
cont = ax.contourf(lon, lat, field, transform=ccrs.PlateCarree())
ax.coastlines()
ax.set_global()
plt.colorbar(cont)
```

A similar example but for a three dimensional field is exported to a [VTK](https://vtk.org/) file, which can be visualized with [ParaView](https://www.paraview.org/) or [PyVista](https://docs.pyvista.org) in Python:
```python
import gstools as gs
# structured field with a size 100x100x100 and a grid-size of 1x1x1
x = y = z = range(100)
model = gs.Gaussian(dim=3, len_scale=[16, 8, 4], angles=(0.8, 0.4, 0.2))
srf = gs.SRF(model)
srf((x, y, z), mesh_type='structured')
srf.vtk_export('3d_field') # Save to a VTK file for ParaView
mesh = srf.to_pyvista() # Create a PyVista mesh for plotting in Python
mesh.contour(isosurfaces=8).plot()
```

## Estimating and Fitting Variograms
The spatial structure of a field can be analyzed with the variogram, which contains the same information as the covariance function.
All covariance models can be used to fit given variogram data by a simple interface.
### Example
This is an example of how to estimate the variogram of a 2 dimensional unstructured field and estimate the parameters of the covariance
model again.
```python
import numpy as np
import gstools as gs
# generate a synthetic field with an exponential model
x = np.random.RandomState(19970221).rand(1000) * 100.
y = np.random.RandomState(20011012).rand(1000) * 100.
model = gs.Exponential(dim=2, var=2, len_scale=8)
srf = gs.SRF(model, mean=0, seed=19970221)
field = srf((x, y))
# estimate the variogram of the field
bin_center, gamma = gs.vario_estimate((x, y), field)
# fit the variogram with a stable model. (no nugget fitted)
fit_model = gs.Stable(dim=2)
fit_model.fit_variogram(bin_center, gamma, nugget=False)
# output
ax = fit_model.plot(x_max=max(bin_center))
ax.scatter(bin_center, gamma)
print(fit_model)
```
Which gives:
```python
Stable(dim=2, var=1.85, len_scale=7.42, nugget=0.0, anis=[1.0], angles=[0.0], alpha=1.09)
```

## Kriging and Conditioned Random Fields
An important part of geostatistics is Kriging and conditioning spatial random
fields to measurements. With conditioned random fields, an ensemble of field realizations with their variability depending on the proximity of the measurements can be generated.
### Example
For better visualization, we will condition a 1d field to a few "measurements", generate 100 realizations and plot them:
```python
import numpy as np
import matplotlib.pyplot as plt
import gstools as gs
# conditions
cond_pos = [0.3, 1.9, 1.1, 3.3, 4.7]
cond_val = [0.47, 0.56, 0.74, 1.47, 1.74]
# conditioned spatial random field class
model = gs.Gaussian(dim=1, var=0.5, len_scale=2)
krige = gs.krige.Ordinary(model, cond_pos, cond_val)
cond_srf = gs.CondSRF(krige)
# same output positions for all ensemble members
grid_pos = np.linspace(0.0, 15.0, 151)
cond_srf.set_pos(grid_pos)
# seeded ensemble generation
seed = gs.random.MasterRNG(20170519)
for i in range(100):
field = cond_srf(seed=seed(), store=f"field_{i}")
plt.plot(grid_pos, field, color="k", alpha=0.1)
plt.scatter(cond_pos, cond_val, color="k")
plt.show()
```

## User Defined Covariance Models
One of the core-features of GSTools is the powerful
[CovModel][cov_link]
class, which allows to easy define covariance models by the user.
### Example
Here we re-implement the Gaussian covariance model by defining just a
[correlation][cor_link] function, which takes a non-dimensional distance ``h = r/l``:
```python
import numpy as np
import gstools as gs
# use CovModel as the base-class
class Gau(gs.CovModel):
def cor(self, h):
return np.exp(-h**2)
```
And that's it! With ``Gau`` you now have a fully working covariance model,
which you could use for field generation or variogram fitting as shown above.
Have a look at the [documentation ][doc_link] for further information on incorporating
optional parameters and optimizations.
## Incompressible Vector Field Generation
Using the original [Kraichnan method][kraichnan_link], incompressible random
spatial vector fields can be generated.
### Example
```python
import numpy as np
import gstools as gs
x = np.arange(100)
y = np.arange(100)
model = gs.Gaussian(dim=2, var=1, len_scale=10)
srf = gs.SRF(model, generator='VectorField', seed=19841203)
srf((x, y), mesh_type='structured')
srf.plot()
```
yielding

[kraichnan_link]: https://doi.org/10.1063/1.1692799
## VTK/PyVista Export
After you have created a field, you may want to save it to file, so we provide
a handy [VTK][vtk_link] export routine using the `.vtk_export()` or you could
create a VTK/PyVista dataset for use in Python with to `.to_pyvista()` method:
```python
import gstools as gs
x = y = range(100)
model = gs.Gaussian(dim=2, var=1, len_scale=10)
srf = gs.SRF(model)
srf((x, y), mesh_type='structured')
srf.vtk_export("field") # Saves to a VTK file
mesh = srf.to_pyvista() # Create a VTK/PyVista dataset in memory
mesh.plot()
```
Which gives a RectilinearGrid VTK file ``field.vtr`` or creates a PyVista mesh
in memory for immediate 3D plotting in Python.

## Requirements:
- [NumPy >= 1.14.5](https://www.numpy.org)
- [SciPy >= 1.1.0](https://www.scipy.org/scipylib)
- [hankel >= 1.0.0](https://github.com/steven-murray/hankel)
- [emcee >= 3.0.0](https://github.com/dfm/emcee)
- [pyevtk >= 1.1.1](https://github.com/pyscience-projects/pyevtk)
- [meshio >= 5.1.0](https://github.com/nschloe/meshio)
### Optional
- [GSTools-Core >= 0.2.0](https://github.com/GeoStat-Framework/GSTools-Core)
- [matplotlib](https://matplotlib.org)
- [pyvista](https://docs.pyvista.org/)
## Contact
You can contact us via .
## License
[LGPLv3][license_link] © 2018-2021
[pip_link]: https://pypi.org/project/gstools
[conda_link]: https://docs.conda.io/en/latest/miniconda.html
[conda_forge_link]: https://github.com/conda-forge/gstools-feedstock#installing-gstools
[conda_pip]: https://docs.conda.io/projects/conda/en/latest/user-guide/tasks/manage-pkgs.html#installing-non-conda-packages
[pipiflag]: https://pip-python3.readthedocs.io/en/latest/reference/pip_install.html?highlight=i#cmdoption-i
[winpy_link]: https://winpython.github.io/
[license_link]: https://github.com/GeoStat-Framework/GSTools/blob/main/LICENSE
[cov_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/generated/gstools.covmodel.CovModel.html#gstools.covmodel.CovModel
[stable_link]: https://en.wikipedia.org/wiki/Stable_distribution
[doc_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/
[doc_install_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/#pip
[tut_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/tutorials.html
[tut1_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/examples/01_random_field/index.html
[tut2_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/examples/02_cov_model/index.html
[tut3_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/examples/03_variogram/index.html
[tut4_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/examples/04_vector_field/index.html
[tut5_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/examples/05_kriging/index.html
[tut6_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/examples/06_conditioned_fields/index.html
[tut7_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/examples/07_transformations/index.html
[tut8_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/examples/08_geo_coordinates/index.html
[tut9_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/examples/09_spatio_temporal/index.html
[tut10_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/examples/10_normalizer/index.html
[tut0_link]: https://geostat-framework.readthedocs.io/projects/gstools/en/stable/examples/00_misc/index.html
[cor_link]: https://en.wikipedia.org/wiki/Autocovariance#Normalization
[vtk_link]: https://www.vtk.org/
%prep
%autosetup -n gstools-1.4.1
%build
%py3_build
%install
%py3_install
install -d -m755 %{buildroot}/%{_pkgdocdir}
if [ -d doc ]; then cp -arf doc %{buildroot}/%{_pkgdocdir}; fi
if [ -d docs ]; then cp -arf docs %{buildroot}/%{_pkgdocdir}; fi
if [ -d example ]; then cp -arf example %{buildroot}/%{_pkgdocdir}; fi
if [ -d examples ]; then cp -arf examples %{buildroot}/%{_pkgdocdir}; fi
pushd %{buildroot}
if [ -d usr/lib ]; then
find usr/lib -type f -printf "/%h/%f\n" >> filelist.lst
fi
if [ -d usr/lib64 ]; then
find usr/lib64 -type f -printf "/%h/%f\n" >> filelist.lst
fi
if [ -d usr/bin ]; then
find usr/bin -type f -printf "/%h/%f\n" >> filelist.lst
fi
if [ -d usr/sbin ]; then
find usr/sbin -type f -printf "/%h/%f\n" >> filelist.lst
fi
touch doclist.lst
if [ -d usr/share/man ]; then
find usr/share/man -type f -printf "/%h/%f.gz\n" >> doclist.lst
fi
popd
mv %{buildroot}/filelist.lst .
mv %{buildroot}/doclist.lst .
%files -n python3-gstools -f filelist.lst
%dir %{python3_sitearch}/*
%files help -f doclist.lst
%{_docdir}/*
%changelog
* Tue Apr 25 2023 Python_Bot - 1.4.1-1
- Package Spec generated


 GeoStatTools provides geostatistical tools for various purposes:
- random field generation
- simple, ordinary, universal and external drift kriging
- conditioned field generation
- incompressible random vector field generation
- (automated) variogram estimation and fitting
- directional variogram estimation and modelling
- data normalization and transformation
- many readily provided and even user-defined covariance models
- metric spatio-temporal modelling
- plotting and exporting routines
## Installation
### conda
GSTools can be installed via [conda][conda_link] on Linux, Mac, and Windows.
Install the package by typing the following command in a command terminal:
conda install gstools
In case conda forge is not set up for your system yet, see the easy to follow
instructions on [conda forge][conda_forge_link]. Using conda, the parallelized
version of GSTools should be installed.
### pip
GSTools can be installed via [pip][pip_link] on Linux, Mac, and Windows.
On Windows you can install [WinPython][winpy_link] to get Python and pip
running. Install the package by typing the following command in a command terminal:
pip install gstools
To install the latest development version via pip, see the
[documentation][doc_install_link].
## Citation
If you are using GSTools in your publication please cite our paper:
> Müller, S., Schüler, L., Zech, A., and Heße, F.:
> GSTools v1.3: a toolbox for geostatistical modelling in Python,
> Geosci. Model Dev., 15, 3161–3182, https://doi.org/10.5194/gmd-15-3161-2022, 2022.
You can cite the Zenodo code publication of GSTools by:
> Sebastian Müller & Lennart Schüler. GeoStat-Framework/GSTools. Zenodo. https://doi.org/10.5281/zenodo.1313628
If you want to cite a specific version, have a look at the [Zenodo site](https://doi.org/10.5281/zenodo.1313628).
## Documentation for GSTools
You can find the documentation under [geostat-framework.readthedocs.io][doc_link].
### Tutorials and Examples
The documentation also includes some [tutorials][tut_link], showing the most important use cases of GSTools, which are
- [Random Field Generation][tut1_link]
- [The Covariance Model][tut2_link]
- [Variogram Estimation][tut3_link]
- [Random Vector Field Generation][tut4_link]
- [Kriging][tut5_link]
- [Conditioned random field generation][tut6_link]
- [Field transformations][tut7_link]
- [Geographic Coordinates][tut8_link]
- [Spatio-Temporal Modelling][tut9_link]
- [Normalizing Data][tut10_link]
- [Miscellaneous examples][tut0_link]
The associated python scripts are provided in the `examples` folder.
## Spatial Random Field Generation
The core of this library is the generation of spatial random fields. These fields are generated using the randomisation method, described by [Heße et al. 2014][rand_link].
[rand_link]: https://doi.org/10.1016/j.envsoft.2014.01.013
### Examples
#### Gaussian Covariance Model
This is an example of how to generate a 2 dimensional spatial random field with a gaussian covariance model.
```python
import gstools as gs
# structured field with a size 100x100 and a grid-size of 1x1
x = y = range(100)
model = gs.Gaussian(dim=2, var=1, len_scale=10)
srf = gs.SRF(model)
srf((x, y), mesh_type='structured')
srf.plot()
```
GeoStatTools provides geostatistical tools for various purposes:
- random field generation
- simple, ordinary, universal and external drift kriging
- conditioned field generation
- incompressible random vector field generation
- (automated) variogram estimation and fitting
- directional variogram estimation and modelling
- data normalization and transformation
- many readily provided and even user-defined covariance models
- metric spatio-temporal modelling
- plotting and exporting routines
## Installation
### conda
GSTools can be installed via [conda][conda_link] on Linux, Mac, and Windows.
Install the package by typing the following command in a command terminal:
conda install gstools
In case conda forge is not set up for your system yet, see the easy to follow
instructions on [conda forge][conda_forge_link]. Using conda, the parallelized
version of GSTools should be installed.
### pip
GSTools can be installed via [pip][pip_link] on Linux, Mac, and Windows.
On Windows you can install [WinPython][winpy_link] to get Python and pip
running. Install the package by typing the following command in a command terminal:
pip install gstools
To install the latest development version via pip, see the
[documentation][doc_install_link].
## Citation
If you are using GSTools in your publication please cite our paper:
> Müller, S., Schüler, L., Zech, A., and Heße, F.:
> GSTools v1.3: a toolbox for geostatistical modelling in Python,
> Geosci. Model Dev., 15, 3161–3182, https://doi.org/10.5194/gmd-15-3161-2022, 2022.
You can cite the Zenodo code publication of GSTools by:
> Sebastian Müller & Lennart Schüler. GeoStat-Framework/GSTools. Zenodo. https://doi.org/10.5281/zenodo.1313628
If you want to cite a specific version, have a look at the [Zenodo site](https://doi.org/10.5281/zenodo.1313628).
## Documentation for GSTools
You can find the documentation under [geostat-framework.readthedocs.io][doc_link].
### Tutorials and Examples
The documentation also includes some [tutorials][tut_link], showing the most important use cases of GSTools, which are
- [Random Field Generation][tut1_link]
- [The Covariance Model][tut2_link]
- [Variogram Estimation][tut3_link]
- [Random Vector Field Generation][tut4_link]
- [Kriging][tut5_link]
- [Conditioned random field generation][tut6_link]
- [Field transformations][tut7_link]
- [Geographic Coordinates][tut8_link]
- [Spatio-Temporal Modelling][tut9_link]
- [Normalizing Data][tut10_link]
- [Miscellaneous examples][tut0_link]
The associated python scripts are provided in the `examples` folder.
## Spatial Random Field Generation
The core of this library is the generation of spatial random fields. These fields are generated using the randomisation method, described by [Heße et al. 2014][rand_link].
[rand_link]: https://doi.org/10.1016/j.envsoft.2014.01.013
### Examples
#### Gaussian Covariance Model
This is an example of how to generate a 2 dimensional spatial random field with a gaussian covariance model.
```python
import gstools as gs
# structured field with a size 100x100 and a grid-size of 1x1
x = y = range(100)
model = gs.Gaussian(dim=2, var=1, len_scale=10)
srf = gs.SRF(model)
srf((x, y), mesh_type='structured')
srf.plot()
```








 GeoStatTools provides geostatistical tools for various purposes:
- random field generation
- simple, ordinary, universal and external drift kriging
- conditioned field generation
- incompressible random vector field generation
- (automated) variogram estimation and fitting
- directional variogram estimation and modelling
- data normalization and transformation
- many readily provided and even user-defined covariance models
- metric spatio-temporal modelling
- plotting and exporting routines
## Installation
### conda
GSTools can be installed via [conda][conda_link] on Linux, Mac, and Windows.
Install the package by typing the following command in a command terminal:
conda install gstools
In case conda forge is not set up for your system yet, see the easy to follow
instructions on [conda forge][conda_forge_link]. Using conda, the parallelized
version of GSTools should be installed.
### pip
GSTools can be installed via [pip][pip_link] on Linux, Mac, and Windows.
On Windows you can install [WinPython][winpy_link] to get Python and pip
running. Install the package by typing the following command in a command terminal:
pip install gstools
To install the latest development version via pip, see the
[documentation][doc_install_link].
## Citation
If you are using GSTools in your publication please cite our paper:
> Müller, S., Schüler, L., Zech, A., and Heße, F.:
> GSTools v1.3: a toolbox for geostatistical modelling in Python,
> Geosci. Model Dev., 15, 3161–3182, https://doi.org/10.5194/gmd-15-3161-2022, 2022.
You can cite the Zenodo code publication of GSTools by:
> Sebastian Müller & Lennart Schüler. GeoStat-Framework/GSTools. Zenodo. https://doi.org/10.5281/zenodo.1313628
If you want to cite a specific version, have a look at the [Zenodo site](https://doi.org/10.5281/zenodo.1313628).
## Documentation for GSTools
You can find the documentation under [geostat-framework.readthedocs.io][doc_link].
### Tutorials and Examples
The documentation also includes some [tutorials][tut_link], showing the most important use cases of GSTools, which are
- [Random Field Generation][tut1_link]
- [The Covariance Model][tut2_link]
- [Variogram Estimation][tut3_link]
- [Random Vector Field Generation][tut4_link]
- [Kriging][tut5_link]
- [Conditioned random field generation][tut6_link]
- [Field transformations][tut7_link]
- [Geographic Coordinates][tut8_link]
- [Spatio-Temporal Modelling][tut9_link]
- [Normalizing Data][tut10_link]
- [Miscellaneous examples][tut0_link]
The associated python scripts are provided in the `examples` folder.
## Spatial Random Field Generation
The core of this library is the generation of spatial random fields. These fields are generated using the randomisation method, described by [Heße et al. 2014][rand_link].
[rand_link]: https://doi.org/10.1016/j.envsoft.2014.01.013
### Examples
#### Gaussian Covariance Model
This is an example of how to generate a 2 dimensional spatial random field with a gaussian covariance model.
```python
import gstools as gs
# structured field with a size 100x100 and a grid-size of 1x1
x = y = range(100)
model = gs.Gaussian(dim=2, var=1, len_scale=10)
srf = gs.SRF(model)
srf((x, y), mesh_type='structured')
srf.plot()
```
GeoStatTools provides geostatistical tools for various purposes:
- random field generation
- simple, ordinary, universal and external drift kriging
- conditioned field generation
- incompressible random vector field generation
- (automated) variogram estimation and fitting
- directional variogram estimation and modelling
- data normalization and transformation
- many readily provided and even user-defined covariance models
- metric spatio-temporal modelling
- plotting and exporting routines
## Installation
### conda
GSTools can be installed via [conda][conda_link] on Linux, Mac, and Windows.
Install the package by typing the following command in a command terminal:
conda install gstools
In case conda forge is not set up for your system yet, see the easy to follow
instructions on [conda forge][conda_forge_link]. Using conda, the parallelized
version of GSTools should be installed.
### pip
GSTools can be installed via [pip][pip_link] on Linux, Mac, and Windows.
On Windows you can install [WinPython][winpy_link] to get Python and pip
running. Install the package by typing the following command in a command terminal:
pip install gstools
To install the latest development version via pip, see the
[documentation][doc_install_link].
## Citation
If you are using GSTools in your publication please cite our paper:
> Müller, S., Schüler, L., Zech, A., and Heße, F.:
> GSTools v1.3: a toolbox for geostatistical modelling in Python,
> Geosci. Model Dev., 15, 3161–3182, https://doi.org/10.5194/gmd-15-3161-2022, 2022.
You can cite the Zenodo code publication of GSTools by:
> Sebastian Müller & Lennart Schüler. GeoStat-Framework/GSTools. Zenodo. https://doi.org/10.5281/zenodo.1313628
If you want to cite a specific version, have a look at the [Zenodo site](https://doi.org/10.5281/zenodo.1313628).
## Documentation for GSTools
You can find the documentation under [geostat-framework.readthedocs.io][doc_link].
### Tutorials and Examples
The documentation also includes some [tutorials][tut_link], showing the most important use cases of GSTools, which are
- [Random Field Generation][tut1_link]
- [The Covariance Model][tut2_link]
- [Variogram Estimation][tut3_link]
- [Random Vector Field Generation][tut4_link]
- [Kriging][tut5_link]
- [Conditioned random field generation][tut6_link]
- [Field transformations][tut7_link]
- [Geographic Coordinates][tut8_link]
- [Spatio-Temporal Modelling][tut9_link]
- [Normalizing Data][tut10_link]
- [Miscellaneous examples][tut0_link]
The associated python scripts are provided in the `examples` folder.
## Spatial Random Field Generation
The core of this library is the generation of spatial random fields. These fields are generated using the randomisation method, described by [Heße et al. 2014][rand_link].
[rand_link]: https://doi.org/10.1016/j.envsoft.2014.01.013
### Examples
#### Gaussian Covariance Model
This is an example of how to generate a 2 dimensional spatial random field with a gaussian covariance model.
```python
import gstools as gs
# structured field with a size 100x100 and a grid-size of 1x1
x = y = range(100)
model = gs.Gaussian(dim=2, var=1, len_scale=10)
srf = gs.SRF(model)
srf((x, y), mesh_type='structured')
srf.plot()
```








 GeoStatTools provides geostatistical tools for various purposes:
- random field generation
- simple, ordinary, universal and external drift kriging
- conditioned field generation
- incompressible random vector field generation
- (automated) variogram estimation and fitting
- directional variogram estimation and modelling
- data normalization and transformation
- many readily provided and even user-defined covariance models
- metric spatio-temporal modelling
- plotting and exporting routines
## Installation
### conda
GSTools can be installed via [conda][conda_link] on Linux, Mac, and Windows.
Install the package by typing the following command in a command terminal:
conda install gstools
In case conda forge is not set up for your system yet, see the easy to follow
instructions on [conda forge][conda_forge_link]. Using conda, the parallelized
version of GSTools should be installed.
### pip
GSTools can be installed via [pip][pip_link] on Linux, Mac, and Windows.
On Windows you can install [WinPython][winpy_link] to get Python and pip
running. Install the package by typing the following command in a command terminal:
pip install gstools
To install the latest development version via pip, see the
[documentation][doc_install_link].
## Citation
If you are using GSTools in your publication please cite our paper:
> Müller, S., Schüler, L., Zech, A., and Heße, F.:
> GSTools v1.3: a toolbox for geostatistical modelling in Python,
> Geosci. Model Dev., 15, 3161–3182, https://doi.org/10.5194/gmd-15-3161-2022, 2022.
You can cite the Zenodo code publication of GSTools by:
> Sebastian Müller & Lennart Schüler. GeoStat-Framework/GSTools. Zenodo. https://doi.org/10.5281/zenodo.1313628
If you want to cite a specific version, have a look at the [Zenodo site](https://doi.org/10.5281/zenodo.1313628).
## Documentation for GSTools
You can find the documentation under [geostat-framework.readthedocs.io][doc_link].
### Tutorials and Examples
The documentation also includes some [tutorials][tut_link], showing the most important use cases of GSTools, which are
- [Random Field Generation][tut1_link]
- [The Covariance Model][tut2_link]
- [Variogram Estimation][tut3_link]
- [Random Vector Field Generation][tut4_link]
- [Kriging][tut5_link]
- [Conditioned random field generation][tut6_link]
- [Field transformations][tut7_link]
- [Geographic Coordinates][tut8_link]
- [Spatio-Temporal Modelling][tut9_link]
- [Normalizing Data][tut10_link]
- [Miscellaneous examples][tut0_link]
The associated python scripts are provided in the `examples` folder.
## Spatial Random Field Generation
The core of this library is the generation of spatial random fields. These fields are generated using the randomisation method, described by [Heße et al. 2014][rand_link].
[rand_link]: https://doi.org/10.1016/j.envsoft.2014.01.013
### Examples
#### Gaussian Covariance Model
This is an example of how to generate a 2 dimensional spatial random field with a gaussian covariance model.
```python
import gstools as gs
# structured field with a size 100x100 and a grid-size of 1x1
x = y = range(100)
model = gs.Gaussian(dim=2, var=1, len_scale=10)
srf = gs.SRF(model)
srf((x, y), mesh_type='structured')
srf.plot()
```
GeoStatTools provides geostatistical tools for various purposes:
- random field generation
- simple, ordinary, universal and external drift kriging
- conditioned field generation
- incompressible random vector field generation
- (automated) variogram estimation and fitting
- directional variogram estimation and modelling
- data normalization and transformation
- many readily provided and even user-defined covariance models
- metric spatio-temporal modelling
- plotting and exporting routines
## Installation
### conda
GSTools can be installed via [conda][conda_link] on Linux, Mac, and Windows.
Install the package by typing the following command in a command terminal:
conda install gstools
In case conda forge is not set up for your system yet, see the easy to follow
instructions on [conda forge][conda_forge_link]. Using conda, the parallelized
version of GSTools should be installed.
### pip
GSTools can be installed via [pip][pip_link] on Linux, Mac, and Windows.
On Windows you can install [WinPython][winpy_link] to get Python and pip
running. Install the package by typing the following command in a command terminal:
pip install gstools
To install the latest development version via pip, see the
[documentation][doc_install_link].
## Citation
If you are using GSTools in your publication please cite our paper:
> Müller, S., Schüler, L., Zech, A., and Heße, F.:
> GSTools v1.3: a toolbox for geostatistical modelling in Python,
> Geosci. Model Dev., 15, 3161–3182, https://doi.org/10.5194/gmd-15-3161-2022, 2022.
You can cite the Zenodo code publication of GSTools by:
> Sebastian Müller & Lennart Schüler. GeoStat-Framework/GSTools. Zenodo. https://doi.org/10.5281/zenodo.1313628
If you want to cite a specific version, have a look at the [Zenodo site](https://doi.org/10.5281/zenodo.1313628).
## Documentation for GSTools
You can find the documentation under [geostat-framework.readthedocs.io][doc_link].
### Tutorials and Examples
The documentation also includes some [tutorials][tut_link], showing the most important use cases of GSTools, which are
- [Random Field Generation][tut1_link]
- [The Covariance Model][tut2_link]
- [Variogram Estimation][tut3_link]
- [Random Vector Field Generation][tut4_link]
- [Kriging][tut5_link]
- [Conditioned random field generation][tut6_link]
- [Field transformations][tut7_link]
- [Geographic Coordinates][tut8_link]
- [Spatio-Temporal Modelling][tut9_link]
- [Normalizing Data][tut10_link]
- [Miscellaneous examples][tut0_link]
The associated python scripts are provided in the `examples` folder.
## Spatial Random Field Generation
The core of this library is the generation of spatial random fields. These fields are generated using the randomisation method, described by [Heße et al. 2014][rand_link].
[rand_link]: https://doi.org/10.1016/j.envsoft.2014.01.013
### Examples
#### Gaussian Covariance Model
This is an example of how to generate a 2 dimensional spatial random field with a gaussian covariance model.
```python
import gstools as gs
# structured field with a size 100x100 and a grid-size of 1x1
x = y = range(100)
model = gs.Gaussian(dim=2, var=1, len_scale=10)
srf = gs.SRF(model)
srf((x, y), mesh_type='structured')
srf.plot()
```






