%global _empty_manifest_terminate_build 0
Name: python-signal-processing-algorithms
Version: 2.0.1
Release: 1
Summary: Signal Processing Algorithms from MongoDB
License: Apache-2.0
URL: https://github.com/mongodb/signal-processing-algorithms
Source0: https://mirrors.nju.edu.cn/pypi/web/packages/79/b9/c212922a7f0d367be1834a3e7c6341594060d3ff37cd8ec95b0a2459efc6/signal-processing-algorithms-2.0.1.tar.gz
BuildArch: noarch
Requires: python3-more-itertools
Requires: python3-numpy
Requires: python3-scipy
Requires: python3-structlog
Requires: python3-typing-extensions
%description
# Signal Processing Algorithms
A suite of algorithms implementing [Energy
Statistics](https://en.wikipedia.org/wiki/Energy_distance), [E-Divisive with
Means](https://arxiv.org/pdf/1306.4933.pdf) and [Generalized ESD Test for
Outliers](https://www.itl.nist.gov/div898/handbook/eda/section3/eda35h3.htm) in python. See [The Use
of Change Point Detection to Identify Software Performance Regressions in a Continuous Integration
System](https://dl.acm.org/doi/abs/10.1145/3358960.3375791) and [Creating a Virtuous Cycle in
Performance Testing at MongoDB](https://dl.acm.org/doi/pdf/10.1145/3427921.3450234) for background
on the development and use of this library.
## Getting Started - Users
```
pip install signal-processing-algorithms
```
## Getting Started - Developers
Getting the code:
```
$ git clone git@github.com:mongodb/signal-processing-algorithms.git
$ cd signal-processing-algorithms
```
Installation
```
$ pip install poetry
$ poetry install
```
Testing/linting:
```
$ poetry run pytest
```
Running the slow tests:
```
$ poetry run pytest --runslow
```
**Some of the larger tests can take a significant amount of time (more than 2 hours).**
## Energy statistics
[Energy Statistics](https://en.wikipedia.org/wiki/Energy_distance) is the statistical concept of Energy Distance
and can be used to measure how similar/different two distributions are.
For statistical samples from two random variables X and Y:
x1, x2, ..., xn and y1, y2, ..., yn
E-Statistic is defined as:
:=2A-B-C) where,
where,
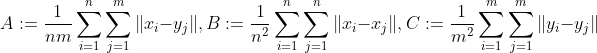 T-statistic is defined as:
T-statistic is defined as:
) E-coefficient of inhomogeneity is defined as:
E-coefficient of inhomogeneity is defined as:
 ```
from signal_processing_algorithms.energy_statistics import energy_statistics
from some_module import series1, series2
# To get Energy Statistics of the distributions.
es = energy_statistics.get_energy_statistics(series1, series2)
# To get Energy Statistics and permutation test results of the distributions.
es_with_probabilities = energy_statistics.get_energy_statistics_and_probabilities(series1, series2, permutations=100)
```
## Intro to E-Divisive
Detecting distributional changes in a series of numerical values can be surprisingly difficult. Simple systems based on thresholds or
mean values can be yield false positives due to outliers in the data, and will fail to detect changes in the noise
profile of the series you are analyzing.
One robust way of detecting many of the changes missed by other approaches is to use [E-Divisive with Means](https://arxiv.org/pdf/1306.4933.pdf), an energy
statistic based approach that compares the expected distance (Euclidean norm) between samples of two portions of the
series with the expected distance between samples within those portions.
That is to say, assuming that the two portions can each be modeled as i.i.d. samples drawn from distinct random variables
(X for the first portion, Y for the second portion), you would expect the E-statistic to be non-zero if there is a
difference between the two portions:
```
from signal_processing_algorithms.energy_statistics import energy_statistics
from some_module import series1, series2
# To get Energy Statistics of the distributions.
es = energy_statistics.get_energy_statistics(series1, series2)
# To get Energy Statistics and permutation test results of the distributions.
es_with_probabilities = energy_statistics.get_energy_statistics_and_probabilities(series1, series2, permutations=100)
```
## Intro to E-Divisive
Detecting distributional changes in a series of numerical values can be surprisingly difficult. Simple systems based on thresholds or
mean values can be yield false positives due to outliers in the data, and will fail to detect changes in the noise
profile of the series you are analyzing.
One robust way of detecting many of the changes missed by other approaches is to use [E-Divisive with Means](https://arxiv.org/pdf/1306.4933.pdf), an energy
statistic based approach that compares the expected distance (Euclidean norm) between samples of two portions of the
series with the expected distance between samples within those portions.
That is to say, assuming that the two portions can each be modeled as i.i.d. samples drawn from distinct random variables
(X for the first portion, Y for the second portion), you would expect the E-statistic to be non-zero if there is a
difference between the two portions:
:=2A-B-C) where A, B and C are as defined in the Energy Statistics above.
One can prove that
where A, B and C are as defined in the Energy Statistics above.
One can prove that \geq&space;0}) and that the corresponding population value is zero if and only if X and Y have the same distribution. Under this null hypothesis the test statistic
and that the corresponding population value is zero if and only if X and Y have the same distribution. Under this null hypothesis the test statistic
) converges in distribution to a quadratic form of independent standard normal random variables. Under the alternative hypothesis T tends to infinity. This makes it possible to construct a consistent statistical test, the energy test for equal distributions
Thus for a series Z of length L,
converges in distribution to a quadratic form of independent standard normal random variables. Under the alternative hypothesis T tends to infinity. This makes it possible to construct a consistent statistical test, the energy test for equal distributions
Thus for a series Z of length L,
 we find the most likely change point by solving the following for τ such that it has the maximum T statistic value.
### Multiple Change Points
The algorithm for finding multiple change points is also simple.
Assuming you have some k known change points:
1. Partition the series into segments between/around these change points.
2. Find the maximum value of our divergence metric _within_ each partition.
3. Take the maximum of the maxima we have just found --> this is our k+1th change point.
4. Return to step 1 and continue until reaching your stopping criterion.
### Stopping Criterion
In this package we have implemented a permutation based test as a stopping criterion:
After step 3 of the multiple change point procedure above, randomly permute all of the data _within_ each cluster, and
find the most likely change point for this permuted data using the procedure laid out above.
After performing this operation z times, count the number of
permuted change points z' that have higher divergence metrics than the change point you calculated with un-permuted data.
The significance level of your change point is thus z'/(z+1).
We allow users to configure a permutation tester with `pvalue`
and `permutations` representing the significance cutoff for algorithm termination and permutations to perform for each
test, respectively.
### Example
```
from signal_processing_algorithms.energy_statistics import energy_statistics
from some_module import series
change_points = energy_statistics.e_divisive(series, pvalue=0.01, permutations=100)
```
%package -n python3-signal-processing-algorithms
Summary: Signal Processing Algorithms from MongoDB
Provides: python-signal-processing-algorithms
BuildRequires: python3-devel
BuildRequires: python3-setuptools
BuildRequires: python3-pip
%description -n python3-signal-processing-algorithms
# Signal Processing Algorithms
A suite of algorithms implementing [Energy
Statistics](https://en.wikipedia.org/wiki/Energy_distance), [E-Divisive with
Means](https://arxiv.org/pdf/1306.4933.pdf) and [Generalized ESD Test for
Outliers](https://www.itl.nist.gov/div898/handbook/eda/section3/eda35h3.htm) in python. See [The Use
of Change Point Detection to Identify Software Performance Regressions in a Continuous Integration
System](https://dl.acm.org/doi/abs/10.1145/3358960.3375791) and [Creating a Virtuous Cycle in
Performance Testing at MongoDB](https://dl.acm.org/doi/pdf/10.1145/3427921.3450234) for background
on the development and use of this library.
## Getting Started - Users
```
pip install signal-processing-algorithms
```
## Getting Started - Developers
Getting the code:
```
$ git clone git@github.com:mongodb/signal-processing-algorithms.git
$ cd signal-processing-algorithms
```
Installation
```
$ pip install poetry
$ poetry install
```
Testing/linting:
```
$ poetry run pytest
```
Running the slow tests:
```
$ poetry run pytest --runslow
```
**Some of the larger tests can take a significant amount of time (more than 2 hours).**
## Energy statistics
[Energy Statistics](https://en.wikipedia.org/wiki/Energy_distance) is the statistical concept of Energy Distance
and can be used to measure how similar/different two distributions are.
For statistical samples from two random variables X and Y:
x1, x2, ..., xn and y1, y2, ..., yn
E-Statistic is defined as:
we find the most likely change point by solving the following for τ such that it has the maximum T statistic value.
### Multiple Change Points
The algorithm for finding multiple change points is also simple.
Assuming you have some k known change points:
1. Partition the series into segments between/around these change points.
2. Find the maximum value of our divergence metric _within_ each partition.
3. Take the maximum of the maxima we have just found --> this is our k+1th change point.
4. Return to step 1 and continue until reaching your stopping criterion.
### Stopping Criterion
In this package we have implemented a permutation based test as a stopping criterion:
After step 3 of the multiple change point procedure above, randomly permute all of the data _within_ each cluster, and
find the most likely change point for this permuted data using the procedure laid out above.
After performing this operation z times, count the number of
permuted change points z' that have higher divergence metrics than the change point you calculated with un-permuted data.
The significance level of your change point is thus z'/(z+1).
We allow users to configure a permutation tester with `pvalue`
and `permutations` representing the significance cutoff for algorithm termination and permutations to perform for each
test, respectively.
### Example
```
from signal_processing_algorithms.energy_statistics import energy_statistics
from some_module import series
change_points = energy_statistics.e_divisive(series, pvalue=0.01, permutations=100)
```
%package -n python3-signal-processing-algorithms
Summary: Signal Processing Algorithms from MongoDB
Provides: python-signal-processing-algorithms
BuildRequires: python3-devel
BuildRequires: python3-setuptools
BuildRequires: python3-pip
%description -n python3-signal-processing-algorithms
# Signal Processing Algorithms
A suite of algorithms implementing [Energy
Statistics](https://en.wikipedia.org/wiki/Energy_distance), [E-Divisive with
Means](https://arxiv.org/pdf/1306.4933.pdf) and [Generalized ESD Test for
Outliers](https://www.itl.nist.gov/div898/handbook/eda/section3/eda35h3.htm) in python. See [The Use
of Change Point Detection to Identify Software Performance Regressions in a Continuous Integration
System](https://dl.acm.org/doi/abs/10.1145/3358960.3375791) and [Creating a Virtuous Cycle in
Performance Testing at MongoDB](https://dl.acm.org/doi/pdf/10.1145/3427921.3450234) for background
on the development and use of this library.
## Getting Started - Users
```
pip install signal-processing-algorithms
```
## Getting Started - Developers
Getting the code:
```
$ git clone git@github.com:mongodb/signal-processing-algorithms.git
$ cd signal-processing-algorithms
```
Installation
```
$ pip install poetry
$ poetry install
```
Testing/linting:
```
$ poetry run pytest
```
Running the slow tests:
```
$ poetry run pytest --runslow
```
**Some of the larger tests can take a significant amount of time (more than 2 hours).**
## Energy statistics
[Energy Statistics](https://en.wikipedia.org/wiki/Energy_distance) is the statistical concept of Energy Distance
and can be used to measure how similar/different two distributions are.
For statistical samples from two random variables X and Y:
x1, x2, ..., xn and y1, y2, ..., yn
E-Statistic is defined as:
:=2A-B-C) where,
where,
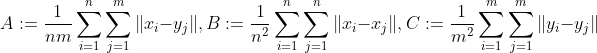 T-statistic is defined as:
T-statistic is defined as:
) E-coefficient of inhomogeneity is defined as:
E-coefficient of inhomogeneity is defined as:
 ```
from signal_processing_algorithms.energy_statistics import energy_statistics
from some_module import series1, series2
# To get Energy Statistics of the distributions.
es = energy_statistics.get_energy_statistics(series1, series2)
# To get Energy Statistics and permutation test results of the distributions.
es_with_probabilities = energy_statistics.get_energy_statistics_and_probabilities(series1, series2, permutations=100)
```
## Intro to E-Divisive
Detecting distributional changes in a series of numerical values can be surprisingly difficult. Simple systems based on thresholds or
mean values can be yield false positives due to outliers in the data, and will fail to detect changes in the noise
profile of the series you are analyzing.
One robust way of detecting many of the changes missed by other approaches is to use [E-Divisive with Means](https://arxiv.org/pdf/1306.4933.pdf), an energy
statistic based approach that compares the expected distance (Euclidean norm) between samples of two portions of the
series with the expected distance between samples within those portions.
That is to say, assuming that the two portions can each be modeled as i.i.d. samples drawn from distinct random variables
(X for the first portion, Y for the second portion), you would expect the E-statistic to be non-zero if there is a
difference between the two portions:
```
from signal_processing_algorithms.energy_statistics import energy_statistics
from some_module import series1, series2
# To get Energy Statistics of the distributions.
es = energy_statistics.get_energy_statistics(series1, series2)
# To get Energy Statistics and permutation test results of the distributions.
es_with_probabilities = energy_statistics.get_energy_statistics_and_probabilities(series1, series2, permutations=100)
```
## Intro to E-Divisive
Detecting distributional changes in a series of numerical values can be surprisingly difficult. Simple systems based on thresholds or
mean values can be yield false positives due to outliers in the data, and will fail to detect changes in the noise
profile of the series you are analyzing.
One robust way of detecting many of the changes missed by other approaches is to use [E-Divisive with Means](https://arxiv.org/pdf/1306.4933.pdf), an energy
statistic based approach that compares the expected distance (Euclidean norm) between samples of two portions of the
series with the expected distance between samples within those portions.
That is to say, assuming that the two portions can each be modeled as i.i.d. samples drawn from distinct random variables
(X for the first portion, Y for the second portion), you would expect the E-statistic to be non-zero if there is a
difference between the two portions:
:=2A-B-C) where A, B and C are as defined in the Energy Statistics above.
One can prove that
where A, B and C are as defined in the Energy Statistics above.
One can prove that \geq&space;0}) and that the corresponding population value is zero if and only if X and Y have the same distribution. Under this null hypothesis the test statistic
and that the corresponding population value is zero if and only if X and Y have the same distribution. Under this null hypothesis the test statistic
) converges in distribution to a quadratic form of independent standard normal random variables. Under the alternative hypothesis T tends to infinity. This makes it possible to construct a consistent statistical test, the energy test for equal distributions
Thus for a series Z of length L,
converges in distribution to a quadratic form of independent standard normal random variables. Under the alternative hypothesis T tends to infinity. This makes it possible to construct a consistent statistical test, the energy test for equal distributions
Thus for a series Z of length L,
 we find the most likely change point by solving the following for τ such that it has the maximum T statistic value.
### Multiple Change Points
The algorithm for finding multiple change points is also simple.
Assuming you have some k known change points:
1. Partition the series into segments between/around these change points.
2. Find the maximum value of our divergence metric _within_ each partition.
3. Take the maximum of the maxima we have just found --> this is our k+1th change point.
4. Return to step 1 and continue until reaching your stopping criterion.
### Stopping Criterion
In this package we have implemented a permutation based test as a stopping criterion:
After step 3 of the multiple change point procedure above, randomly permute all of the data _within_ each cluster, and
find the most likely change point for this permuted data using the procedure laid out above.
After performing this operation z times, count the number of
permuted change points z' that have higher divergence metrics than the change point you calculated with un-permuted data.
The significance level of your change point is thus z'/(z+1).
We allow users to configure a permutation tester with `pvalue`
and `permutations` representing the significance cutoff for algorithm termination and permutations to perform for each
test, respectively.
### Example
```
from signal_processing_algorithms.energy_statistics import energy_statistics
from some_module import series
change_points = energy_statistics.e_divisive(series, pvalue=0.01, permutations=100)
```
%package help
Summary: Development documents and examples for signal-processing-algorithms
Provides: python3-signal-processing-algorithms-doc
%description help
# Signal Processing Algorithms
A suite of algorithms implementing [Energy
Statistics](https://en.wikipedia.org/wiki/Energy_distance), [E-Divisive with
Means](https://arxiv.org/pdf/1306.4933.pdf) and [Generalized ESD Test for
Outliers](https://www.itl.nist.gov/div898/handbook/eda/section3/eda35h3.htm) in python. See [The Use
of Change Point Detection to Identify Software Performance Regressions in a Continuous Integration
System](https://dl.acm.org/doi/abs/10.1145/3358960.3375791) and [Creating a Virtuous Cycle in
Performance Testing at MongoDB](https://dl.acm.org/doi/pdf/10.1145/3427921.3450234) for background
on the development and use of this library.
## Getting Started - Users
```
pip install signal-processing-algorithms
```
## Getting Started - Developers
Getting the code:
```
$ git clone git@github.com:mongodb/signal-processing-algorithms.git
$ cd signal-processing-algorithms
```
Installation
```
$ pip install poetry
$ poetry install
```
Testing/linting:
```
$ poetry run pytest
```
Running the slow tests:
```
$ poetry run pytest --runslow
```
**Some of the larger tests can take a significant amount of time (more than 2 hours).**
## Energy statistics
[Energy Statistics](https://en.wikipedia.org/wiki/Energy_distance) is the statistical concept of Energy Distance
and can be used to measure how similar/different two distributions are.
For statistical samples from two random variables X and Y:
x1, x2, ..., xn and y1, y2, ..., yn
E-Statistic is defined as:
we find the most likely change point by solving the following for τ such that it has the maximum T statistic value.
### Multiple Change Points
The algorithm for finding multiple change points is also simple.
Assuming you have some k known change points:
1. Partition the series into segments between/around these change points.
2. Find the maximum value of our divergence metric _within_ each partition.
3. Take the maximum of the maxima we have just found --> this is our k+1th change point.
4. Return to step 1 and continue until reaching your stopping criterion.
### Stopping Criterion
In this package we have implemented a permutation based test as a stopping criterion:
After step 3 of the multiple change point procedure above, randomly permute all of the data _within_ each cluster, and
find the most likely change point for this permuted data using the procedure laid out above.
After performing this operation z times, count the number of
permuted change points z' that have higher divergence metrics than the change point you calculated with un-permuted data.
The significance level of your change point is thus z'/(z+1).
We allow users to configure a permutation tester with `pvalue`
and `permutations` representing the significance cutoff for algorithm termination and permutations to perform for each
test, respectively.
### Example
```
from signal_processing_algorithms.energy_statistics import energy_statistics
from some_module import series
change_points = energy_statistics.e_divisive(series, pvalue=0.01, permutations=100)
```
%package help
Summary: Development documents and examples for signal-processing-algorithms
Provides: python3-signal-processing-algorithms-doc
%description help
# Signal Processing Algorithms
A suite of algorithms implementing [Energy
Statistics](https://en.wikipedia.org/wiki/Energy_distance), [E-Divisive with
Means](https://arxiv.org/pdf/1306.4933.pdf) and [Generalized ESD Test for
Outliers](https://www.itl.nist.gov/div898/handbook/eda/section3/eda35h3.htm) in python. See [The Use
of Change Point Detection to Identify Software Performance Regressions in a Continuous Integration
System](https://dl.acm.org/doi/abs/10.1145/3358960.3375791) and [Creating a Virtuous Cycle in
Performance Testing at MongoDB](https://dl.acm.org/doi/pdf/10.1145/3427921.3450234) for background
on the development and use of this library.
## Getting Started - Users
```
pip install signal-processing-algorithms
```
## Getting Started - Developers
Getting the code:
```
$ git clone git@github.com:mongodb/signal-processing-algorithms.git
$ cd signal-processing-algorithms
```
Installation
```
$ pip install poetry
$ poetry install
```
Testing/linting:
```
$ poetry run pytest
```
Running the slow tests:
```
$ poetry run pytest --runslow
```
**Some of the larger tests can take a significant amount of time (more than 2 hours).**
## Energy statistics
[Energy Statistics](https://en.wikipedia.org/wiki/Energy_distance) is the statistical concept of Energy Distance
and can be used to measure how similar/different two distributions are.
For statistical samples from two random variables X and Y:
x1, x2, ..., xn and y1, y2, ..., yn
E-Statistic is defined as:
:=2A-B-C) where,
where,
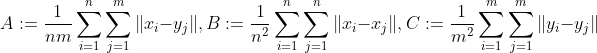 T-statistic is defined as:
T-statistic is defined as:
) E-coefficient of inhomogeneity is defined as:
E-coefficient of inhomogeneity is defined as:
 ```
from signal_processing_algorithms.energy_statistics import energy_statistics
from some_module import series1, series2
# To get Energy Statistics of the distributions.
es = energy_statistics.get_energy_statistics(series1, series2)
# To get Energy Statistics and permutation test results of the distributions.
es_with_probabilities = energy_statistics.get_energy_statistics_and_probabilities(series1, series2, permutations=100)
```
## Intro to E-Divisive
Detecting distributional changes in a series of numerical values can be surprisingly difficult. Simple systems based on thresholds or
mean values can be yield false positives due to outliers in the data, and will fail to detect changes in the noise
profile of the series you are analyzing.
One robust way of detecting many of the changes missed by other approaches is to use [E-Divisive with Means](https://arxiv.org/pdf/1306.4933.pdf), an energy
statistic based approach that compares the expected distance (Euclidean norm) between samples of two portions of the
series with the expected distance between samples within those portions.
That is to say, assuming that the two portions can each be modeled as i.i.d. samples drawn from distinct random variables
(X for the first portion, Y for the second portion), you would expect the E-statistic to be non-zero if there is a
difference between the two portions:
```
from signal_processing_algorithms.energy_statistics import energy_statistics
from some_module import series1, series2
# To get Energy Statistics of the distributions.
es = energy_statistics.get_energy_statistics(series1, series2)
# To get Energy Statistics and permutation test results of the distributions.
es_with_probabilities = energy_statistics.get_energy_statistics_and_probabilities(series1, series2, permutations=100)
```
## Intro to E-Divisive
Detecting distributional changes in a series of numerical values can be surprisingly difficult. Simple systems based on thresholds or
mean values can be yield false positives due to outliers in the data, and will fail to detect changes in the noise
profile of the series you are analyzing.
One robust way of detecting many of the changes missed by other approaches is to use [E-Divisive with Means](https://arxiv.org/pdf/1306.4933.pdf), an energy
statistic based approach that compares the expected distance (Euclidean norm) between samples of two portions of the
series with the expected distance between samples within those portions.
That is to say, assuming that the two portions can each be modeled as i.i.d. samples drawn from distinct random variables
(X for the first portion, Y for the second portion), you would expect the E-statistic to be non-zero if there is a
difference between the two portions:
:=2A-B-C) where A, B and C are as defined in the Energy Statistics above.
One can prove that
where A, B and C are as defined in the Energy Statistics above.
One can prove that \geq&space;0}) and that the corresponding population value is zero if and only if X and Y have the same distribution. Under this null hypothesis the test statistic
and that the corresponding population value is zero if and only if X and Y have the same distribution. Under this null hypothesis the test statistic
) converges in distribution to a quadratic form of independent standard normal random variables. Under the alternative hypothesis T tends to infinity. This makes it possible to construct a consistent statistical test, the energy test for equal distributions
Thus for a series Z of length L,
converges in distribution to a quadratic form of independent standard normal random variables. Under the alternative hypothesis T tends to infinity. This makes it possible to construct a consistent statistical test, the energy test for equal distributions
Thus for a series Z of length L,
 we find the most likely change point by solving the following for τ such that it has the maximum T statistic value.
### Multiple Change Points
The algorithm for finding multiple change points is also simple.
Assuming you have some k known change points:
1. Partition the series into segments between/around these change points.
2. Find the maximum value of our divergence metric _within_ each partition.
3. Take the maximum of the maxima we have just found --> this is our k+1th change point.
4. Return to step 1 and continue until reaching your stopping criterion.
### Stopping Criterion
In this package we have implemented a permutation based test as a stopping criterion:
After step 3 of the multiple change point procedure above, randomly permute all of the data _within_ each cluster, and
find the most likely change point for this permuted data using the procedure laid out above.
After performing this operation z times, count the number of
permuted change points z' that have higher divergence metrics than the change point you calculated with un-permuted data.
The significance level of your change point is thus z'/(z+1).
We allow users to configure a permutation tester with `pvalue`
and `permutations` representing the significance cutoff for algorithm termination and permutations to perform for each
test, respectively.
### Example
```
from signal_processing_algorithms.energy_statistics import energy_statistics
from some_module import series
change_points = energy_statistics.e_divisive(series, pvalue=0.01, permutations=100)
```
%prep
%autosetup -n signal-processing-algorithms-2.0.1
%build
%py3_build
%install
%py3_install
install -d -m755 %{buildroot}/%{_pkgdocdir}
if [ -d doc ]; then cp -arf doc %{buildroot}/%{_pkgdocdir}; fi
if [ -d docs ]; then cp -arf docs %{buildroot}/%{_pkgdocdir}; fi
if [ -d example ]; then cp -arf example %{buildroot}/%{_pkgdocdir}; fi
if [ -d examples ]; then cp -arf examples %{buildroot}/%{_pkgdocdir}; fi
pushd %{buildroot}
if [ -d usr/lib ]; then
find usr/lib -type f -printf "/%h/%f\n" >> filelist.lst
fi
if [ -d usr/lib64 ]; then
find usr/lib64 -type f -printf "/%h/%f\n" >> filelist.lst
fi
if [ -d usr/bin ]; then
find usr/bin -type f -printf "/%h/%f\n" >> filelist.lst
fi
if [ -d usr/sbin ]; then
find usr/sbin -type f -printf "/%h/%f\n" >> filelist.lst
fi
touch doclist.lst
if [ -d usr/share/man ]; then
find usr/share/man -type f -printf "/%h/%f.gz\n" >> doclist.lst
fi
popd
mv %{buildroot}/filelist.lst .
mv %{buildroot}/doclist.lst .
%files -n python3-signal-processing-algorithms -f filelist.lst
%dir %{python3_sitelib}/*
%files help -f doclist.lst
%{_docdir}/*
%changelog
* Wed Apr 12 2023 Python_Bot - 2.0.1-1
- Package Spec generated
we find the most likely change point by solving the following for τ such that it has the maximum T statistic value.
### Multiple Change Points
The algorithm for finding multiple change points is also simple.
Assuming you have some k known change points:
1. Partition the series into segments between/around these change points.
2. Find the maximum value of our divergence metric _within_ each partition.
3. Take the maximum of the maxima we have just found --> this is our k+1th change point.
4. Return to step 1 and continue until reaching your stopping criterion.
### Stopping Criterion
In this package we have implemented a permutation based test as a stopping criterion:
After step 3 of the multiple change point procedure above, randomly permute all of the data _within_ each cluster, and
find the most likely change point for this permuted data using the procedure laid out above.
After performing this operation z times, count the number of
permuted change points z' that have higher divergence metrics than the change point you calculated with un-permuted data.
The significance level of your change point is thus z'/(z+1).
We allow users to configure a permutation tester with `pvalue`
and `permutations` representing the significance cutoff for algorithm termination and permutations to perform for each
test, respectively.
### Example
```
from signal_processing_algorithms.energy_statistics import energy_statistics
from some_module import series
change_points = energy_statistics.e_divisive(series, pvalue=0.01, permutations=100)
```
%prep
%autosetup -n signal-processing-algorithms-2.0.1
%build
%py3_build
%install
%py3_install
install -d -m755 %{buildroot}/%{_pkgdocdir}
if [ -d doc ]; then cp -arf doc %{buildroot}/%{_pkgdocdir}; fi
if [ -d docs ]; then cp -arf docs %{buildroot}/%{_pkgdocdir}; fi
if [ -d example ]; then cp -arf example %{buildroot}/%{_pkgdocdir}; fi
if [ -d examples ]; then cp -arf examples %{buildroot}/%{_pkgdocdir}; fi
pushd %{buildroot}
if [ -d usr/lib ]; then
find usr/lib -type f -printf "/%h/%f\n" >> filelist.lst
fi
if [ -d usr/lib64 ]; then
find usr/lib64 -type f -printf "/%h/%f\n" >> filelist.lst
fi
if [ -d usr/bin ]; then
find usr/bin -type f -printf "/%h/%f\n" >> filelist.lst
fi
if [ -d usr/sbin ]; then
find usr/sbin -type f -printf "/%h/%f\n" >> filelist.lst
fi
touch doclist.lst
if [ -d usr/share/man ]; then
find usr/share/man -type f -printf "/%h/%f.gz\n" >> doclist.lst
fi
popd
mv %{buildroot}/filelist.lst .
mv %{buildroot}/doclist.lst .
%files -n python3-signal-processing-algorithms -f filelist.lst
%dir %{python3_sitelib}/*
%files help -f doclist.lst
%{_docdir}/*
%changelog
* Wed Apr 12 2023 Python_Bot - 2.0.1-1
- Package Spec generated