diff options
| author | CoprDistGit <infra@openeuler.org> | 2023-05-05 12:20:53 +0000 |
|---|---|---|
| committer | CoprDistGit <infra@openeuler.org> | 2023-05-05 12:20:53 +0000 |
| commit | 743453f29661257776520a1de885978da5f667ea (patch) | |
| tree | 93dfcfeef0fc164860d52d20dcf78e4d9011e327 | |
| parent | 3e897a29b610671ff4cbed89c9ef56c86a335b41 (diff) | |
automatic import of python-egttoolsopeneuler20.03
| -rw-r--r-- | .gitignore | 1 | ||||
| -rw-r--r-- | python-egttools.spec | 1255 | ||||
| -rw-r--r-- | sources | 1 |
3 files changed, 1257 insertions, 0 deletions
@@ -0,0 +1 @@ +/egttools-0.1.12.tar.gz diff --git a/python-egttools.spec b/python-egttools.spec new file mode 100644 index 0000000..2f3e4da --- /dev/null +++ b/python-egttools.spec @@ -0,0 +1,1255 @@ +%global _empty_manifest_terminate_build 0 +Name: python-egttools +Version: 0.1.12 +Release: 1 +Summary: Efficient Python library for EGT +License: GPLv3 +URL: https://github.com/Socrats/EGTTools +Source0: https://mirrors.nju.edu.cn/pypi/web/packages/77/d5/c9ab5709f13caa6b94595abb9b4ba484c8419eb018a568c59d7f1a962cea/egttools-0.1.12.tar.gz + +Requires: python3-numpy +Requires: python3-scipy +Requires: python3-matplotlib +Requires: python3-networkx +Requires: python3-seaborn + +%description + + +# Toolbox for Evolutionary Game Theory + +[](https://badge.fury.io/py/egttools) +[](https://egttools.readthedocs.io/en/latest/?badge=latest) +[](https://github.com/Socrats/EGTTools/actions/workflows/ci.yml) [](https://gitter.im/EGTTools/community?utm_source=badge&utm_medium=badge&utm_campaign=pr-badge&utm_content=badge) +[](https://mybinder.org/v2/gh/Socrats/EGTTools/HEAD?labpath=docs%2Fexamples) +[](https://zenodo.org/badge/latestdoi/242180332) + +[//]: # ([](https://pypi.org/project/egttools/)) + +**EGTtools** provides a centralized repository with analytical and numerical methods to study/model game theoretical +problems under the Evolutionary Game Theory (EGT) framework. + +This library is composed of two parts: + +- a set of analytical methods implemented in Python 3 +- a set of computational methods implemented in C++ with (Python 3 bindings) + +The second typed is used in cases where the state space is too big to solve analytically, and thus require estimating +the model parameters through monte-carlo simulations. The C++ implementation provides optimized computational methods +that can run in parallel in a reasonable time, while Python bindings make the methods easily accecible to a larger range +of researchers. + +## Table of Contents + +1. [Requirements](#requirements) +2. [Downloading sources](#downloading-sources) +3. [Examples of usage](#examples-of-usage) +4. [Documentation](#documentation) +5. [Caveats](#caveats) +6. [Citing](#citing) +7. [Licence](#licence) +8. [Acknowledgements](#acknowledgements) + +## Requirements + +To be able to install EGTtools, you must have: + +* A recent version of Linux (only tested on Ubuntu), MacOSX (Mojave or above) or Windows +* [**CMake**](https://cmake.org) version 3.17 or higher +* [**C++ 17**](https://en.cppreference.com/w/cpp/17) +* [**Eigen**](https://eigen.tuxfamily.org/index.php?title=Main_Page) 3.3.* +* [**Boost**](https://www.boost.org/) 1.80.* +* **Python** 3.7 or higher +* If you want support for parallel operations you should install [**OpenMP**](https://www.openmp.org) +* Ideally, you should also install [**OpenBLAS**](https://www.openblas.net), which offers optimized implementations of + linear algebra kernels for several processor architectures, and install numpy and scipy versions that use it. + +## Downloading sources + +When cloning the repository you should also clone the submodules so that pybind11 is downloaded. You can do that by +running: + +```bash +git clone --recurse-submodules -j8 https://github.com/Socrats/EGTTools.git +``` + +## Installation + +### With pip + +You can install `egttools` directly from PyPi with: + +```bash +pip install egttools +``` + +Currently, only the Linux build supports OpenMP parallelization for numerical simulations. This should normally be ok +for most applications, since numerical simulations are heavy and should be run on High Power Computing (HPC) clusters +which normally run Linux distributions. + +We are investigating how to provide support for OpenMP in both Windows and Mac. In the meantime, if you really want to +run numerical simulations on either of the two platforms, you should follow the compilation instructions below and try +to link OpenMP for your platform yourself. Please, if you manage to do so, open an issue or a pull request with your +solutions. + +**Note**: For Apple M1 (arm64) you should install using ```pip install egttools --no-deps``` so that pip does not +install the dependencies of the package. You should then install these dependencies through a virtual environment +created with [miniforge](https://github.com/conda-forge/miniforge) (see [Caveats](#caveats) for more information on why +this is necessary). Once you have miniforge installed you can do the following (assuming that you are in the base +miniforge environment): + +```bash +conda create -n egtenv python=3.9 +conda activate egtenv +conda install numpy +conda install scipy +conda install matplotlib +conda install networkx +conda install seaborn +``` + +### Build from source + +To build `egttools` from source follow the following steps. + +To **install all required packages** run: + +```bash +python -m venv egttools-env +source egttools-env/bin/activate +pip install -r requirements.txt +``` + +Or with anaconda: + +```bash +conda env create -f environment.yml +conda activate egttools-env +``` + +Also, to make your virtual environment visible to jupyter: + +```bash +conda install ipykernel # or pip install ipykernel +python -m ipykernel install --user --name=egttools-env +``` + +You can **build EGTtools** in your virtual environment by running: + +```bash +pip install build +cd <path> +python -m build +``` + +Where ```<path>``` represents the path to the EGTtools folder. If you are running this while inside the EGTtools folder, +then ```<path>``` is simply ```./```. + +Finally, you can install EGTtools in **development** mode, this will allow the installation to update with new +modifications to the package: + +```bash +python -m pip install -e <path> +``` + +If you don't want development mode, you can skip the option ```-e```. + +## Examples of usage + +The [Analytical example](docs/examples/hawk_dove_dynamics.ipynb) is a jupyter notebook which analyses analytically the +evolutionary dynamics in a (2-person, 2-actions, one-shot) Hawk-Dove game. + +The [Numerical example](docs/examples/normal_form_game_mc_simulations.ipynb) is a jupyter notebook which analyses +through numerical simulations the evolutionary dynamics in a (2-person, 2-actions, one-shot) Hawk-Dove game. + +The [Invasion example](docs/examples/plot_invasion_diagram.ipynb) is a jupyter notebook calculates the fixation +probabilities and stationary distribution of a Normal Form Game with 5 strategies and then plots an invasion diagram. + +The [Plot 2 Simplex](docs/examples/plot_simplex.ipynb) is a jupyter notebook that shows how to use EGTtools to plot the +evolutionary dynamics in a 2 Simplex (a triangle), both for infinite and finite populations. + +You can also check all these notebooks and a bit more on +this [tutorial repository](https://github.com/Socrats/egt-tutorial) + +For example, assuming the following payoff matrix: + + + +You can plot the gradient of selection in a finite population of \(Z=100\) individuals and assuming and intensity of +selection 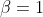 in the following way: + +```python +import numpy as np +from egttools.analytical import PairwiseComparison +from egttools.games import Matrix2PlayerGameHolder + +beta = 1; Z = 100; nb_strategies = 2; A = np.array([[-0.5, 2.], [0., 0.]]) +pop_states = np.arange(0, Z + 1, 1) + +game = Matrix2PlayerGameHolder(nb_strategies, payoff_matrix=A) + +# Instantiate evolver and calculate gradient +evolver = PairwiseComparison(population_size=Z, game=game) +gradients = np.array([evolver.calculate_gradient_of_selection(beta, np.array([x, Z-x])) for x in range(Z + 1)]) +``` + +Afterwards, you can plot the results with: + +```python +from egttools.plotting import plot_gradients +plot_gradients(gradients, figsize=(4,4), fig_title="Hawk-Dove game stochastic dynamics", + marker_facecolor='white', + xlabel="frequency of hawks (k/Z)", marker="o", marker_size=20, marker_plot_freq=2) +``` + + + +And you can plot the stationary distribution for a mutation +rate  with: + +```python +import matplotlib.pyplot as plt +from egttools.utils import calculate_stationary_distribution + +transitions = evolver.calculate_transition_matrix(beta, mu=1e-3) +stationary_with_mu = calculate_stationary_distribution(transitions.transpose()) +fig, ax = plt.subplots(figsize=(5, 4)) +fig.patch.set_facecolor('white') +lines = ax.plot(np.arange(0, Z + 1) / Z, stationary_with_mu) +plt.setp(lines, linewidth=2.0) +ax.set_ylabel('stationary distribution', size=16) +ax.set_xlabel('$k/Z$', size=16) +ax.set_xlim(0, 1) +plt.show() +``` + + + +We can obtain the same results through numerical simulations. The error will depend on how many independent simulations +you perform and for how long you let the simulation run. While a future implementation will offer an adaptive method to +vary these parameters depending on the variations between the estimated distributions, for the moment it is important +that you let the simulation run for enough generations after it has achieved a steady state. Here is a comparison +between analytical and numerical results: + +```python +from egttools.numerical import PairwiseComparisonNumerical +from egttools.games import NormalFormGame + +# Instantiate the game +game = NormalFormGame(1, A) +numerical_evolver = PairwiseComparisonNumerical(Z, game, 1000000) + +# We do this for different betas +betas = np.logspace(-4, 1, 50) +stationary_points = [] +# numerical simulations +for i in range(len(betas)): + stationary_points.append(numerical_evolver.stationary_distribution(30, int(1e6), int(1e3), + betas[i], 1e-3)) +stationary_points = np.asarray(stationary_points) +# Now we estimate the probability of Cooperation for each possible state +state_frequencies = np.arange(0, Z + 1) / Z +coop_level = np.dot(state_frequencies, stationary_points.T) +``` + +Lastly, we plot the results: + +```python +from sklearn.metrics import mean_squared_error + +mse = mean_squared_error(1 - coop_level_analytical, coop_level) + +# Finally, we plot and compare visually (and check how much error we get) +fig, ax = plt.subplots(figsize=(7, 5)) +# ax.scatter(betas, coop_level, label="simulation") +ax.scatter(betas, coop_level_analytical, marker='x', label="analytical") +ax.scatter(betas, coop_level, marker='o', label="simulation") +ax.text(0.01, 0.535, 'MSE = {0:.3e}'.format(mse), style='italic', + bbox={'facecolor': 'red', 'alpha': 0.5, 'pad': 10}) +ax.legend() +ax.set_xlabel(r'$\beta$', fontsize=15) +ax.set_ylabel('Cooperation level', fontsize=15) +ax.set_xscale('log') +plt.show() +``` + + + +Finally, you may also visualize the result of independent simulations: + +```python +init_states = np.random.randint(0, Z + 1, size=10, dtype=np.uint64) +output = [] +for i in range(10): + output.append(evolver.run(int(1e6), 1, 1e-3, + [init_states[i], Z - init_states[i]])) +# Plot each year's time series in its own facet +fig, ax = plt.subplots(figsize=(5, 4)) + +for run in output: + ax.plot(run[:, 0] / Z, color='gray', linewidth=.1, alpha=0.6) +ax.set_ylabel('k/Z') +ax.set_xlabel('generation') +ax.set_xscale('log') +``` + + + +### Plotting the dynamics in a 2 Simplex + +EGTtools can also be used to visualize the evolutionary dynamics in a 2 Simplex. In the example bellow, we use the +`egttools.plotting.plot_replicator_dynamics_in_simplex` which calculates the gradients on a simplex given an initial +payoff matrix and returns a `egttools.plotting.Simplex2D` object which can be used to plot the 2 Simplex. + +```python +import numpy as np +import matplotlib.pyplot as plt +from egttools.plotting import plot_replicator_dynamics_in_simplex + +payoffs = np.array([[1, 0, 0], + [0, 2, 0], + [0, 0, 3]]) +type_labels = ['A', 'B', 'C'] + +fig, ax = plt.subplots(figsize=(10, 8)) + +simplex, gradient_function, roots, roots_xy, stability = plot_replicator_dynamics_in_simplex(payoffs, ax=ax) + +plot = (simplex.add_axis(ax=ax) + .draw_triangle() + .draw_gradients(zorder=0) + .add_colorbar() + .add_vertex_labels(type_labels) + .draw_stationary_points(roots_xy, stability) + .draw_trajectory_from_roots(gradient_function, + roots, + stability, + trajectory_length=15, + linewidth=1, + step=0.01, + color='k', draw_arrow=True, + arrowdirection='right', + arrowsize=30, zorder=4, arrowstyle='fancy') + .draw_scatter_shadow(gradient_function, 300, color='gray', marker='.', s=0.1, zorder=0) + ) + +ax.axis('off') +ax.set_aspect('equal') + +plt.xlim((-.05, 1.05)) +plt.ylim((-.02, simplex.top_corner + 0.05)) +plt.show() +``` + + + +The same can be done for finite populations, with the added possibility to plot the stationary distribution inside the +triangle (see [simplex plotting](docs/examples/plot_simplex.ipynb) +and [simplified simplex plotting](docs/examples/plot_simplex_simplified.ipynb) +for a more in depth examples). + +## Documentation + +The [analytical](src/egttools/analytical/sed_analytical.py) module contains classes and functions that you may use to +investigate the evolutionary dynamics in N-player games. For now only the replicator dynamics (for infinite populations) +and the Pairwise Comparison imitation process (for finite populations) are implemented. + +When your state-space is too big (in finite populations), it might become computationally hard to solve the system +analytically. Thus, we provide an efficient [numerical](cpp/src/egttools.cpp) module written in C++ and compiled to +Python. You may use it to estimate the fixation probabilities and stationary distribution through Monte-Carlo +simulations, or perform individual runs of the Moran process. + +You can find more information in the [ReadTheDocs](https://egttools.readthedocs.io/en/latest/) documentation. + +### Caveats + +1. On Apple M1 (arm64) you should install (for the moment) [miniforge](https://github.com/conda-forge/miniforge), create + a conda environment using it, and install EGTtools from the conda environment. + +2. In MacOSX it is assumed that you have [Homebrew](https://brew.sh) installed. +3. You should install libomp with homebrew ``brew install libomp`` if you want to have support for parallel operations ( + there is a big difference in computation time). + +4. You **must** have Eigen 3.3.* installed. + +5. You **do not** need any of the above if you install EGTtools through ```pip install egttools --no-deps```. However, + on Apple M1 (arm64) you still need to install the dependencies through miniforge, since only there you can find a + scipy wheel that supports this architecture. + +## Citing + +You may cite this repository in the following way: + +```latex +@misc{Fernandez2020, + author = {Fernández Domingos, Elias}, + title = {EGTTools: Toolbox for Evolutionary Game Theory}, + year = {2020}, + publisher = {GitHub}, + journal = {GitHub repository}, + howpublished = {\url{https://github.com/Socrats/EGTTools}}, + doi = {10.5281/zenodo.3687125} +} +``` + +## Licence + +* EGTtools is released under the [GNU General Public Licence](LICENSE), version 3 or later. +* [pybind11](https://github.com/pybind/pybind11) is released under [a BSD-style license](pybind11/LICENSE). + +## Acknowledgements + +* Great parts of this project have been possible thanks to the help of + [Yannick Jadoul](https://github.com/YannickJadoul) author of + [Parselmouth](https://github.com/YannickJadoul/Parselmouth) + and [Eugenio Bargiacchi](https://github.com/Svalorzen) author of [AIToolBox](https://github.com/Svalorzen/AI-Toolbox). + They are both great programmers and scientists, so it is always a good idea to check out their work. +* EGTtools makes use of the amazing [pybind11](https://github.com/pybind/pybind11). library to provide a Python + interface for optimized monte-carlo simulations written in C++. + + +%package -n python3-egttools +Summary: Efficient Python library for EGT +Provides: python-egttools +BuildRequires: python3-devel +BuildRequires: python3-setuptools +BuildRequires: python3-pip +BuildRequires: python3-cffi +BuildRequires: gcc +BuildRequires: gdb +%description -n python3-egttools + + +# Toolbox for Evolutionary Game Theory + +[](https://badge.fury.io/py/egttools) +[](https://egttools.readthedocs.io/en/latest/?badge=latest) +[](https://github.com/Socrats/EGTTools/actions/workflows/ci.yml) [](https://gitter.im/EGTTools/community?utm_source=badge&utm_medium=badge&utm_campaign=pr-badge&utm_content=badge) +[](https://mybinder.org/v2/gh/Socrats/EGTTools/HEAD?labpath=docs%2Fexamples) +[](https://zenodo.org/badge/latestdoi/242180332) + +[//]: # ([](https://pypi.org/project/egttools/)) + +**EGTtools** provides a centralized repository with analytical and numerical methods to study/model game theoretical +problems under the Evolutionary Game Theory (EGT) framework. + +This library is composed of two parts: + +- a set of analytical methods implemented in Python 3 +- a set of computational methods implemented in C++ with (Python 3 bindings) + +The second typed is used in cases where the state space is too big to solve analytically, and thus require estimating +the model parameters through monte-carlo simulations. The C++ implementation provides optimized computational methods +that can run in parallel in a reasonable time, while Python bindings make the methods easily accecible to a larger range +of researchers. + +## Table of Contents + +1. [Requirements](#requirements) +2. [Downloading sources](#downloading-sources) +3. [Examples of usage](#examples-of-usage) +4. [Documentation](#documentation) +5. [Caveats](#caveats) +6. [Citing](#citing) +7. [Licence](#licence) +8. [Acknowledgements](#acknowledgements) + +## Requirements + +To be able to install EGTtools, you must have: + +* A recent version of Linux (only tested on Ubuntu), MacOSX (Mojave or above) or Windows +* [**CMake**](https://cmake.org) version 3.17 or higher +* [**C++ 17**](https://en.cppreference.com/w/cpp/17) +* [**Eigen**](https://eigen.tuxfamily.org/index.php?title=Main_Page) 3.3.* +* [**Boost**](https://www.boost.org/) 1.80.* +* **Python** 3.7 or higher +* If you want support for parallel operations you should install [**OpenMP**](https://www.openmp.org) +* Ideally, you should also install [**OpenBLAS**](https://www.openblas.net), which offers optimized implementations of + linear algebra kernels for several processor architectures, and install numpy and scipy versions that use it. + +## Downloading sources + +When cloning the repository you should also clone the submodules so that pybind11 is downloaded. You can do that by +running: + +```bash +git clone --recurse-submodules -j8 https://github.com/Socrats/EGTTools.git +``` + +## Installation + +### With pip + +You can install `egttools` directly from PyPi with: + +```bash +pip install egttools +``` + +Currently, only the Linux build supports OpenMP parallelization for numerical simulations. This should normally be ok +for most applications, since numerical simulations are heavy and should be run on High Power Computing (HPC) clusters +which normally run Linux distributions. + +We are investigating how to provide support for OpenMP in both Windows and Mac. In the meantime, if you really want to +run numerical simulations on either of the two platforms, you should follow the compilation instructions below and try +to link OpenMP for your platform yourself. Please, if you manage to do so, open an issue or a pull request with your +solutions. + +**Note**: For Apple M1 (arm64) you should install using ```pip install egttools --no-deps``` so that pip does not +install the dependencies of the package. You should then install these dependencies through a virtual environment +created with [miniforge](https://github.com/conda-forge/miniforge) (see [Caveats](#caveats) for more information on why +this is necessary). Once you have miniforge installed you can do the following (assuming that you are in the base +miniforge environment): + +```bash +conda create -n egtenv python=3.9 +conda activate egtenv +conda install numpy +conda install scipy +conda install matplotlib +conda install networkx +conda install seaborn +``` + +### Build from source + +To build `egttools` from source follow the following steps. + +To **install all required packages** run: + +```bash +python -m venv egttools-env +source egttools-env/bin/activate +pip install -r requirements.txt +``` + +Or with anaconda: + +```bash +conda env create -f environment.yml +conda activate egttools-env +``` + +Also, to make your virtual environment visible to jupyter: + +```bash +conda install ipykernel # or pip install ipykernel +python -m ipykernel install --user --name=egttools-env +``` + +You can **build EGTtools** in your virtual environment by running: + +```bash +pip install build +cd <path> +python -m build +``` + +Where ```<path>``` represents the path to the EGTtools folder. If you are running this while inside the EGTtools folder, +then ```<path>``` is simply ```./```. + +Finally, you can install EGTtools in **development** mode, this will allow the installation to update with new +modifications to the package: + +```bash +python -m pip install -e <path> +``` + +If you don't want development mode, you can skip the option ```-e```. + +## Examples of usage + +The [Analytical example](docs/examples/hawk_dove_dynamics.ipynb) is a jupyter notebook which analyses analytically the +evolutionary dynamics in a (2-person, 2-actions, one-shot) Hawk-Dove game. + +The [Numerical example](docs/examples/normal_form_game_mc_simulations.ipynb) is a jupyter notebook which analyses +through numerical simulations the evolutionary dynamics in a (2-person, 2-actions, one-shot) Hawk-Dove game. + +The [Invasion example](docs/examples/plot_invasion_diagram.ipynb) is a jupyter notebook calculates the fixation +probabilities and stationary distribution of a Normal Form Game with 5 strategies and then plots an invasion diagram. + +The [Plot 2 Simplex](docs/examples/plot_simplex.ipynb) is a jupyter notebook that shows how to use EGTtools to plot the +evolutionary dynamics in a 2 Simplex (a triangle), both for infinite and finite populations. + +You can also check all these notebooks and a bit more on +this [tutorial repository](https://github.com/Socrats/egt-tutorial) + +For example, assuming the following payoff matrix: + + + +You can plot the gradient of selection in a finite population of \(Z=100\) individuals and assuming and intensity of +selection 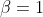 in the following way: + +```python +import numpy as np +from egttools.analytical import PairwiseComparison +from egttools.games import Matrix2PlayerGameHolder + +beta = 1; Z = 100; nb_strategies = 2; A = np.array([[-0.5, 2.], [0., 0.]]) +pop_states = np.arange(0, Z + 1, 1) + +game = Matrix2PlayerGameHolder(nb_strategies, payoff_matrix=A) + +# Instantiate evolver and calculate gradient +evolver = PairwiseComparison(population_size=Z, game=game) +gradients = np.array([evolver.calculate_gradient_of_selection(beta, np.array([x, Z-x])) for x in range(Z + 1)]) +``` + +Afterwards, you can plot the results with: + +```python +from egttools.plotting import plot_gradients +plot_gradients(gradients, figsize=(4,4), fig_title="Hawk-Dove game stochastic dynamics", + marker_facecolor='white', + xlabel="frequency of hawks (k/Z)", marker="o", marker_size=20, marker_plot_freq=2) +``` + + + +And you can plot the stationary distribution for a mutation +rate  with: + +```python +import matplotlib.pyplot as plt +from egttools.utils import calculate_stationary_distribution + +transitions = evolver.calculate_transition_matrix(beta, mu=1e-3) +stationary_with_mu = calculate_stationary_distribution(transitions.transpose()) +fig, ax = plt.subplots(figsize=(5, 4)) +fig.patch.set_facecolor('white') +lines = ax.plot(np.arange(0, Z + 1) / Z, stationary_with_mu) +plt.setp(lines, linewidth=2.0) +ax.set_ylabel('stationary distribution', size=16) +ax.set_xlabel('$k/Z$', size=16) +ax.set_xlim(0, 1) +plt.show() +``` + + + +We can obtain the same results through numerical simulations. The error will depend on how many independent simulations +you perform and for how long you let the simulation run. While a future implementation will offer an adaptive method to +vary these parameters depending on the variations between the estimated distributions, for the moment it is important +that you let the simulation run for enough generations after it has achieved a steady state. Here is a comparison +between analytical and numerical results: + +```python +from egttools.numerical import PairwiseComparisonNumerical +from egttools.games import NormalFormGame + +# Instantiate the game +game = NormalFormGame(1, A) +numerical_evolver = PairwiseComparisonNumerical(Z, game, 1000000) + +# We do this for different betas +betas = np.logspace(-4, 1, 50) +stationary_points = [] +# numerical simulations +for i in range(len(betas)): + stationary_points.append(numerical_evolver.stationary_distribution(30, int(1e6), int(1e3), + betas[i], 1e-3)) +stationary_points = np.asarray(stationary_points) +# Now we estimate the probability of Cooperation for each possible state +state_frequencies = np.arange(0, Z + 1) / Z +coop_level = np.dot(state_frequencies, stationary_points.T) +``` + +Lastly, we plot the results: + +```python +from sklearn.metrics import mean_squared_error + +mse = mean_squared_error(1 - coop_level_analytical, coop_level) + +# Finally, we plot and compare visually (and check how much error we get) +fig, ax = plt.subplots(figsize=(7, 5)) +# ax.scatter(betas, coop_level, label="simulation") +ax.scatter(betas, coop_level_analytical, marker='x', label="analytical") +ax.scatter(betas, coop_level, marker='o', label="simulation") +ax.text(0.01, 0.535, 'MSE = {0:.3e}'.format(mse), style='italic', + bbox={'facecolor': 'red', 'alpha': 0.5, 'pad': 10}) +ax.legend() +ax.set_xlabel(r'$\beta$', fontsize=15) +ax.set_ylabel('Cooperation level', fontsize=15) +ax.set_xscale('log') +plt.show() +``` + + + +Finally, you may also visualize the result of independent simulations: + +```python +init_states = np.random.randint(0, Z + 1, size=10, dtype=np.uint64) +output = [] +for i in range(10): + output.append(evolver.run(int(1e6), 1, 1e-3, + [init_states[i], Z - init_states[i]])) +# Plot each year's time series in its own facet +fig, ax = plt.subplots(figsize=(5, 4)) + +for run in output: + ax.plot(run[:, 0] / Z, color='gray', linewidth=.1, alpha=0.6) +ax.set_ylabel('k/Z') +ax.set_xlabel('generation') +ax.set_xscale('log') +``` + + + +### Plotting the dynamics in a 2 Simplex + +EGTtools can also be used to visualize the evolutionary dynamics in a 2 Simplex. In the example bellow, we use the +`egttools.plotting.plot_replicator_dynamics_in_simplex` which calculates the gradients on a simplex given an initial +payoff matrix and returns a `egttools.plotting.Simplex2D` object which can be used to plot the 2 Simplex. + +```python +import numpy as np +import matplotlib.pyplot as plt +from egttools.plotting import plot_replicator_dynamics_in_simplex + +payoffs = np.array([[1, 0, 0], + [0, 2, 0], + [0, 0, 3]]) +type_labels = ['A', 'B', 'C'] + +fig, ax = plt.subplots(figsize=(10, 8)) + +simplex, gradient_function, roots, roots_xy, stability = plot_replicator_dynamics_in_simplex(payoffs, ax=ax) + +plot = (simplex.add_axis(ax=ax) + .draw_triangle() + .draw_gradients(zorder=0) + .add_colorbar() + .add_vertex_labels(type_labels) + .draw_stationary_points(roots_xy, stability) + .draw_trajectory_from_roots(gradient_function, + roots, + stability, + trajectory_length=15, + linewidth=1, + step=0.01, + color='k', draw_arrow=True, + arrowdirection='right', + arrowsize=30, zorder=4, arrowstyle='fancy') + .draw_scatter_shadow(gradient_function, 300, color='gray', marker='.', s=0.1, zorder=0) + ) + +ax.axis('off') +ax.set_aspect('equal') + +plt.xlim((-.05, 1.05)) +plt.ylim((-.02, simplex.top_corner + 0.05)) +plt.show() +``` + + + +The same can be done for finite populations, with the added possibility to plot the stationary distribution inside the +triangle (see [simplex plotting](docs/examples/plot_simplex.ipynb) +and [simplified simplex plotting](docs/examples/plot_simplex_simplified.ipynb) +for a more in depth examples). + +## Documentation + +The [analytical](src/egttools/analytical/sed_analytical.py) module contains classes and functions that you may use to +investigate the evolutionary dynamics in N-player games. For now only the replicator dynamics (for infinite populations) +and the Pairwise Comparison imitation process (for finite populations) are implemented. + +When your state-space is too big (in finite populations), it might become computationally hard to solve the system +analytically. Thus, we provide an efficient [numerical](cpp/src/egttools.cpp) module written in C++ and compiled to +Python. You may use it to estimate the fixation probabilities and stationary distribution through Monte-Carlo +simulations, or perform individual runs of the Moran process. + +You can find more information in the [ReadTheDocs](https://egttools.readthedocs.io/en/latest/) documentation. + +### Caveats + +1. On Apple M1 (arm64) you should install (for the moment) [miniforge](https://github.com/conda-forge/miniforge), create + a conda environment using it, and install EGTtools from the conda environment. + +2. In MacOSX it is assumed that you have [Homebrew](https://brew.sh) installed. +3. You should install libomp with homebrew ``brew install libomp`` if you want to have support for parallel operations ( + there is a big difference in computation time). + +4. You **must** have Eigen 3.3.* installed. + +5. You **do not** need any of the above if you install EGTtools through ```pip install egttools --no-deps```. However, + on Apple M1 (arm64) you still need to install the dependencies through miniforge, since only there you can find a + scipy wheel that supports this architecture. + +## Citing + +You may cite this repository in the following way: + +```latex +@misc{Fernandez2020, + author = {Fernández Domingos, Elias}, + title = {EGTTools: Toolbox for Evolutionary Game Theory}, + year = {2020}, + publisher = {GitHub}, + journal = {GitHub repository}, + howpublished = {\url{https://github.com/Socrats/EGTTools}}, + doi = {10.5281/zenodo.3687125} +} +``` + +## Licence + +* EGTtools is released under the [GNU General Public Licence](LICENSE), version 3 or later. +* [pybind11](https://github.com/pybind/pybind11) is released under [a BSD-style license](pybind11/LICENSE). + +## Acknowledgements + +* Great parts of this project have been possible thanks to the help of + [Yannick Jadoul](https://github.com/YannickJadoul) author of + [Parselmouth](https://github.com/YannickJadoul/Parselmouth) + and [Eugenio Bargiacchi](https://github.com/Svalorzen) author of [AIToolBox](https://github.com/Svalorzen/AI-Toolbox). + They are both great programmers and scientists, so it is always a good idea to check out their work. +* EGTtools makes use of the amazing [pybind11](https://github.com/pybind/pybind11). library to provide a Python + interface for optimized monte-carlo simulations written in C++. + + +%package help +Summary: Development documents and examples for egttools +Provides: python3-egttools-doc +%description help + + +# Toolbox for Evolutionary Game Theory + +[](https://badge.fury.io/py/egttools) +[](https://egttools.readthedocs.io/en/latest/?badge=latest) +[](https://github.com/Socrats/EGTTools/actions/workflows/ci.yml) [](https://gitter.im/EGTTools/community?utm_source=badge&utm_medium=badge&utm_campaign=pr-badge&utm_content=badge) +[](https://mybinder.org/v2/gh/Socrats/EGTTools/HEAD?labpath=docs%2Fexamples) +[](https://zenodo.org/badge/latestdoi/242180332) + +[//]: # ([](https://pypi.org/project/egttools/)) + +**EGTtools** provides a centralized repository with analytical and numerical methods to study/model game theoretical +problems under the Evolutionary Game Theory (EGT) framework. + +This library is composed of two parts: + +- a set of analytical methods implemented in Python 3 +- a set of computational methods implemented in C++ with (Python 3 bindings) + +The second typed is used in cases where the state space is too big to solve analytically, and thus require estimating +the model parameters through monte-carlo simulations. The C++ implementation provides optimized computational methods +that can run in parallel in a reasonable time, while Python bindings make the methods easily accecible to a larger range +of researchers. + +## Table of Contents + +1. [Requirements](#requirements) +2. [Downloading sources](#downloading-sources) +3. [Examples of usage](#examples-of-usage) +4. [Documentation](#documentation) +5. [Caveats](#caveats) +6. [Citing](#citing) +7. [Licence](#licence) +8. [Acknowledgements](#acknowledgements) + +## Requirements + +To be able to install EGTtools, you must have: + +* A recent version of Linux (only tested on Ubuntu), MacOSX (Mojave or above) or Windows +* [**CMake**](https://cmake.org) version 3.17 or higher +* [**C++ 17**](https://en.cppreference.com/w/cpp/17) +* [**Eigen**](https://eigen.tuxfamily.org/index.php?title=Main_Page) 3.3.* +* [**Boost**](https://www.boost.org/) 1.80.* +* **Python** 3.7 or higher +* If you want support for parallel operations you should install [**OpenMP**](https://www.openmp.org) +* Ideally, you should also install [**OpenBLAS**](https://www.openblas.net), which offers optimized implementations of + linear algebra kernels for several processor architectures, and install numpy and scipy versions that use it. + +## Downloading sources + +When cloning the repository you should also clone the submodules so that pybind11 is downloaded. You can do that by +running: + +```bash +git clone --recurse-submodules -j8 https://github.com/Socrats/EGTTools.git +``` + +## Installation + +### With pip + +You can install `egttools` directly from PyPi with: + +```bash +pip install egttools +``` + +Currently, only the Linux build supports OpenMP parallelization for numerical simulations. This should normally be ok +for most applications, since numerical simulations are heavy and should be run on High Power Computing (HPC) clusters +which normally run Linux distributions. + +We are investigating how to provide support for OpenMP in both Windows and Mac. In the meantime, if you really want to +run numerical simulations on either of the two platforms, you should follow the compilation instructions below and try +to link OpenMP for your platform yourself. Please, if you manage to do so, open an issue or a pull request with your +solutions. + +**Note**: For Apple M1 (arm64) you should install using ```pip install egttools --no-deps``` so that pip does not +install the dependencies of the package. You should then install these dependencies through a virtual environment +created with [miniforge](https://github.com/conda-forge/miniforge) (see [Caveats](#caveats) for more information on why +this is necessary). Once you have miniforge installed you can do the following (assuming that you are in the base +miniforge environment): + +```bash +conda create -n egtenv python=3.9 +conda activate egtenv +conda install numpy +conda install scipy +conda install matplotlib +conda install networkx +conda install seaborn +``` + +### Build from source + +To build `egttools` from source follow the following steps. + +To **install all required packages** run: + +```bash +python -m venv egttools-env +source egttools-env/bin/activate +pip install -r requirements.txt +``` + +Or with anaconda: + +```bash +conda env create -f environment.yml +conda activate egttools-env +``` + +Also, to make your virtual environment visible to jupyter: + +```bash +conda install ipykernel # or pip install ipykernel +python -m ipykernel install --user --name=egttools-env +``` + +You can **build EGTtools** in your virtual environment by running: + +```bash +pip install build +cd <path> +python -m build +``` + +Where ```<path>``` represents the path to the EGTtools folder. If you are running this while inside the EGTtools folder, +then ```<path>``` is simply ```./```. + +Finally, you can install EGTtools in **development** mode, this will allow the installation to update with new +modifications to the package: + +```bash +python -m pip install -e <path> +``` + +If you don't want development mode, you can skip the option ```-e```. + +## Examples of usage + +The [Analytical example](docs/examples/hawk_dove_dynamics.ipynb) is a jupyter notebook which analyses analytically the +evolutionary dynamics in a (2-person, 2-actions, one-shot) Hawk-Dove game. + +The [Numerical example](docs/examples/normal_form_game_mc_simulations.ipynb) is a jupyter notebook which analyses +through numerical simulations the evolutionary dynamics in a (2-person, 2-actions, one-shot) Hawk-Dove game. + +The [Invasion example](docs/examples/plot_invasion_diagram.ipynb) is a jupyter notebook calculates the fixation +probabilities and stationary distribution of a Normal Form Game with 5 strategies and then plots an invasion diagram. + +The [Plot 2 Simplex](docs/examples/plot_simplex.ipynb) is a jupyter notebook that shows how to use EGTtools to plot the +evolutionary dynamics in a 2 Simplex (a triangle), both for infinite and finite populations. + +You can also check all these notebooks and a bit more on +this [tutorial repository](https://github.com/Socrats/egt-tutorial) + +For example, assuming the following payoff matrix: + + + +You can plot the gradient of selection in a finite population of \(Z=100\) individuals and assuming and intensity of +selection 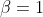 in the following way: + +```python +import numpy as np +from egttools.analytical import PairwiseComparison +from egttools.games import Matrix2PlayerGameHolder + +beta = 1; Z = 100; nb_strategies = 2; A = np.array([[-0.5, 2.], [0., 0.]]) +pop_states = np.arange(0, Z + 1, 1) + +game = Matrix2PlayerGameHolder(nb_strategies, payoff_matrix=A) + +# Instantiate evolver and calculate gradient +evolver = PairwiseComparison(population_size=Z, game=game) +gradients = np.array([evolver.calculate_gradient_of_selection(beta, np.array([x, Z-x])) for x in range(Z + 1)]) +``` + +Afterwards, you can plot the results with: + +```python +from egttools.plotting import plot_gradients +plot_gradients(gradients, figsize=(4,4), fig_title="Hawk-Dove game stochastic dynamics", + marker_facecolor='white', + xlabel="frequency of hawks (k/Z)", marker="o", marker_size=20, marker_plot_freq=2) +``` + + + +And you can plot the stationary distribution for a mutation +rate  with: + +```python +import matplotlib.pyplot as plt +from egttools.utils import calculate_stationary_distribution + +transitions = evolver.calculate_transition_matrix(beta, mu=1e-3) +stationary_with_mu = calculate_stationary_distribution(transitions.transpose()) +fig, ax = plt.subplots(figsize=(5, 4)) +fig.patch.set_facecolor('white') +lines = ax.plot(np.arange(0, Z + 1) / Z, stationary_with_mu) +plt.setp(lines, linewidth=2.0) +ax.set_ylabel('stationary distribution', size=16) +ax.set_xlabel('$k/Z$', size=16) +ax.set_xlim(0, 1) +plt.show() +``` + + + +We can obtain the same results through numerical simulations. The error will depend on how many independent simulations +you perform and for how long you let the simulation run. While a future implementation will offer an adaptive method to +vary these parameters depending on the variations between the estimated distributions, for the moment it is important +that you let the simulation run for enough generations after it has achieved a steady state. Here is a comparison +between analytical and numerical results: + +```python +from egttools.numerical import PairwiseComparisonNumerical +from egttools.games import NormalFormGame + +# Instantiate the game +game = NormalFormGame(1, A) +numerical_evolver = PairwiseComparisonNumerical(Z, game, 1000000) + +# We do this for different betas +betas = np.logspace(-4, 1, 50) +stationary_points = [] +# numerical simulations +for i in range(len(betas)): + stationary_points.append(numerical_evolver.stationary_distribution(30, int(1e6), int(1e3), + betas[i], 1e-3)) +stationary_points = np.asarray(stationary_points) +# Now we estimate the probability of Cooperation for each possible state +state_frequencies = np.arange(0, Z + 1) / Z +coop_level = np.dot(state_frequencies, stationary_points.T) +``` + +Lastly, we plot the results: + +```python +from sklearn.metrics import mean_squared_error + +mse = mean_squared_error(1 - coop_level_analytical, coop_level) + +# Finally, we plot and compare visually (and check how much error we get) +fig, ax = plt.subplots(figsize=(7, 5)) +# ax.scatter(betas, coop_level, label="simulation") +ax.scatter(betas, coop_level_analytical, marker='x', label="analytical") +ax.scatter(betas, coop_level, marker='o', label="simulation") +ax.text(0.01, 0.535, 'MSE = {0:.3e}'.format(mse), style='italic', + bbox={'facecolor': 'red', 'alpha': 0.5, 'pad': 10}) +ax.legend() +ax.set_xlabel(r'$\beta$', fontsize=15) +ax.set_ylabel('Cooperation level', fontsize=15) +ax.set_xscale('log') +plt.show() +``` + + + +Finally, you may also visualize the result of independent simulations: + +```python +init_states = np.random.randint(0, Z + 1, size=10, dtype=np.uint64) +output = [] +for i in range(10): + output.append(evolver.run(int(1e6), 1, 1e-3, + [init_states[i], Z - init_states[i]])) +# Plot each year's time series in its own facet +fig, ax = plt.subplots(figsize=(5, 4)) + +for run in output: + ax.plot(run[:, 0] / Z, color='gray', linewidth=.1, alpha=0.6) +ax.set_ylabel('k/Z') +ax.set_xlabel('generation') +ax.set_xscale('log') +``` + + + +### Plotting the dynamics in a 2 Simplex + +EGTtools can also be used to visualize the evolutionary dynamics in a 2 Simplex. In the example bellow, we use the +`egttools.plotting.plot_replicator_dynamics_in_simplex` which calculates the gradients on a simplex given an initial +payoff matrix and returns a `egttools.plotting.Simplex2D` object which can be used to plot the 2 Simplex. + +```python +import numpy as np +import matplotlib.pyplot as plt +from egttools.plotting import plot_replicator_dynamics_in_simplex + +payoffs = np.array([[1, 0, 0], + [0, 2, 0], + [0, 0, 3]]) +type_labels = ['A', 'B', 'C'] + +fig, ax = plt.subplots(figsize=(10, 8)) + +simplex, gradient_function, roots, roots_xy, stability = plot_replicator_dynamics_in_simplex(payoffs, ax=ax) + +plot = (simplex.add_axis(ax=ax) + .draw_triangle() + .draw_gradients(zorder=0) + .add_colorbar() + .add_vertex_labels(type_labels) + .draw_stationary_points(roots_xy, stability) + .draw_trajectory_from_roots(gradient_function, + roots, + stability, + trajectory_length=15, + linewidth=1, + step=0.01, + color='k', draw_arrow=True, + arrowdirection='right', + arrowsize=30, zorder=4, arrowstyle='fancy') + .draw_scatter_shadow(gradient_function, 300, color='gray', marker='.', s=0.1, zorder=0) + ) + +ax.axis('off') +ax.set_aspect('equal') + +plt.xlim((-.05, 1.05)) +plt.ylim((-.02, simplex.top_corner + 0.05)) +plt.show() +``` + + + +The same can be done for finite populations, with the added possibility to plot the stationary distribution inside the +triangle (see [simplex plotting](docs/examples/plot_simplex.ipynb) +and [simplified simplex plotting](docs/examples/plot_simplex_simplified.ipynb) +for a more in depth examples). + +## Documentation + +The [analytical](src/egttools/analytical/sed_analytical.py) module contains classes and functions that you may use to +investigate the evolutionary dynamics in N-player games. For now only the replicator dynamics (for infinite populations) +and the Pairwise Comparison imitation process (for finite populations) are implemented. + +When your state-space is too big (in finite populations), it might become computationally hard to solve the system +analytically. Thus, we provide an efficient [numerical](cpp/src/egttools.cpp) module written in C++ and compiled to +Python. You may use it to estimate the fixation probabilities and stationary distribution through Monte-Carlo +simulations, or perform individual runs of the Moran process. + +You can find more information in the [ReadTheDocs](https://egttools.readthedocs.io/en/latest/) documentation. + +### Caveats + +1. On Apple M1 (arm64) you should install (for the moment) [miniforge](https://github.com/conda-forge/miniforge), create + a conda environment using it, and install EGTtools from the conda environment. + +2. In MacOSX it is assumed that you have [Homebrew](https://brew.sh) installed. +3. You should install libomp with homebrew ``brew install libomp`` if you want to have support for parallel operations ( + there is a big difference in computation time). + +4. You **must** have Eigen 3.3.* installed. + +5. You **do not** need any of the above if you install EGTtools through ```pip install egttools --no-deps```. However, + on Apple M1 (arm64) you still need to install the dependencies through miniforge, since only there you can find a + scipy wheel that supports this architecture. + +## Citing + +You may cite this repository in the following way: + +```latex +@misc{Fernandez2020, + author = {Fernández Domingos, Elias}, + title = {EGTTools: Toolbox for Evolutionary Game Theory}, + year = {2020}, + publisher = {GitHub}, + journal = {GitHub repository}, + howpublished = {\url{https://github.com/Socrats/EGTTools}}, + doi = {10.5281/zenodo.3687125} +} +``` + +## Licence + +* EGTtools is released under the [GNU General Public Licence](LICENSE), version 3 or later. +* [pybind11](https://github.com/pybind/pybind11) is released under [a BSD-style license](pybind11/LICENSE). + +## Acknowledgements + +* Great parts of this project have been possible thanks to the help of + [Yannick Jadoul](https://github.com/YannickJadoul) author of + [Parselmouth](https://github.com/YannickJadoul/Parselmouth) + and [Eugenio Bargiacchi](https://github.com/Svalorzen) author of [AIToolBox](https://github.com/Svalorzen/AI-Toolbox). + They are both great programmers and scientists, so it is always a good idea to check out their work. +* EGTtools makes use of the amazing [pybind11](https://github.com/pybind/pybind11). library to provide a Python + interface for optimized monte-carlo simulations written in C++. + + +%prep +%autosetup -n egttools-0.1.12 + +%build +%py3_build + +%install +%py3_install +install -d -m755 %{buildroot}/%{_pkgdocdir} +if [ -d doc ]; then cp -arf doc %{buildroot}/%{_pkgdocdir}; fi +if [ -d docs ]; then cp -arf docs %{buildroot}/%{_pkgdocdir}; fi +if [ -d example ]; then cp -arf example %{buildroot}/%{_pkgdocdir}; fi +if [ -d examples ]; then cp -arf examples %{buildroot}/%{_pkgdocdir}; fi +pushd %{buildroot} +if [ -d usr/lib ]; then + find usr/lib -type f -printf "/%h/%f\n" >> filelist.lst +fi +if [ -d usr/lib64 ]; then + find usr/lib64 -type f -printf "/%h/%f\n" >> filelist.lst +fi +if [ -d usr/bin ]; then + find usr/bin -type f -printf "/%h/%f\n" >> filelist.lst +fi +if [ -d usr/sbin ]; then + find usr/sbin -type f -printf "/%h/%f\n" >> filelist.lst +fi +touch doclist.lst +if [ -d usr/share/man ]; then + find usr/share/man -type f -printf "/%h/%f.gz\n" >> doclist.lst +fi +popd +mv %{buildroot}/filelist.lst . +mv %{buildroot}/doclist.lst . + +%files -n python3-egttools -f filelist.lst +%dir %{python3_sitearch}/* + +%files help -f doclist.lst +%{_docdir}/* + +%changelog +* Fri May 05 2023 Python_Bot <Python_Bot@openeuler.org> - 0.1.12-1 +- Package Spec generated @@ -0,0 +1 @@ +47c5eb7ca81c7184567dd2131a911ac6 egttools-0.1.12.tar.gz |
